Bonjour
Pour la première question : tu as fait une démonstration ou tu as seulement (mal) recopié une formule trouvée sur le net ? Tu peux expliqué ton raisonnement ?
Ensuite, tu ne précises pas si de l'air est emprisonné entre le couvercle et le liquide. On pourrait imaginer de poser le couvercle avec un récipient cylindrique rempli d'eau "à ras bord"... Dans tous les cas un schéma légendé serait le bienvenu.

Bonsoir,
finalement j'ai trouvé une autre formule qui est :

avec S la section du réservoir et St la section du petit tube (ou l'eau passe) pour cela, j'ai utilisé la loi de Torriccelli :et j'ai fait - la section S intégrale entre h0 et h  de .

Ensuite, ce n'est pas précisé dans l'énoncé si de l'air est emprisonné, et le réservoir est rempli mais non pas à ras-bord.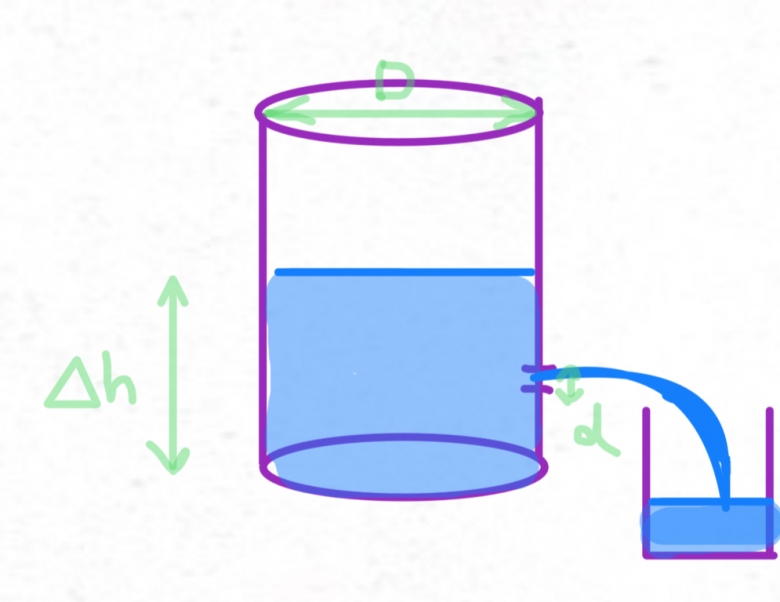



***balises LATEX ajoutées***

Bonsoir,

@fdxsjvo : il faut que tu utilises les balises LATEX pour que tes formules soient lisibles, je ne vais pas repasser à chaque fois sur les messages :

extrait de la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?

Oui, cela est même encouragé.

Les correcteurs sont généralement plus attirés par un message bien écrit en Latex et bien présenté que par un message écrit avec les caractères normaux, non aéré, etc.

Le Latex est un outil mathématique qui pouvait nous permettre à tous de faciliter la lecture et la compréhension en écrivant proprement nos formules mathématiques. Nous vous invitons à prendre connaissance du guide latex présent sur le site. Un tutorial complet vous aide à faire vos premiers pas.
Bien-sûr, l'utilisation du Latex n'est pas obligatoire, mais pourquoi se priver d'un tel outil ?

Si ce langage vous semble trop compliqué à utiliser dans un premier temps, il vous est cependant possible d'insérer très simplement des caractères mathématiques dans votre texte en utilisant l'outil présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le mode d'emploi du forum.

Je pense que tu recopies des formules vues sur le net sans vraiment les comprendre... La dernière formule que tu fournis est directement copiée ; tu ne t'es pas donnée la peine de l'adapter aux notations de l'énoncé et cette formule fournit la date t correspondant à une hauteur h de liquide restant dans le réservoir pour une hauteur initiale h_o. Ce n'est pas la durée totale de vidange demandée par l'énoncé... Il n'y avait pas grand chose à changer dans la formule que tu as fournie la première fois...
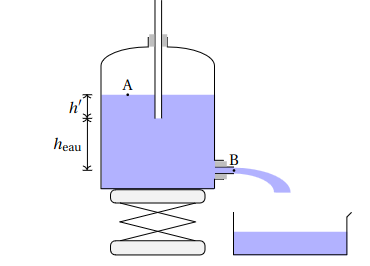
Pour la suite, j'imagine que le schéma ressemble sensiblement à celui-ci. A toi de l'adapter.
Méthode possible : appliquer le théorème de Bernoulli entre A et B puis entre A et l'extrémité basse du tube en considérant le tube de section suffisamment faible devant celle du réservoir pour considérer que la vitesse du fluide en A est pratiquement égale à la vitesse du fluide à l'altitude de l'extrémité inférieure du tube.

Merci pour vos pistes, mais je ne vois toujours pas quoi changer de plus dans ma première formule.

Quelle est la relation simple entre le rapport des aires des sections droites et le rapport des diamètres ?

A₁/A₂= (d₁/d₂)² car l'aire A= (π *d²)/4 ?

Oui. Il fallait donc élever au carré le rapport des deux diamètres dans ta première formule.

D'accord, je vois merci beaucoup pour cette précision !