Bonsoir,

chute dans le plan XZ !

Vx = k*z + Vxo;
Vxo = 0;
x = k*z*t + xo
xo = 0 d'après énoncé

Vz = -g*t + Vzo
Vzo = vo d'après énoncé
z = -1/2 g*t^2 + vo*t + zo
zo = o d'après énoncé

x = k*z*t
z = -1/2 g*t^2 + vo*t

4/
angle et rayon de courbure
arctan(z/x) = arctan(1/k*t)
Rc^2 = x^2 + z^2

Bien avant que Magisterien ne poste, je me posais cette question :

Bien vu . Mea Culpa. Ca m'apprendra à répondre trop vite.
Je trouvais aussi curieux que le moment cinétique soit nulle dans mon cas.

(t) = k.z(t).dt et avec l'expression de z(t) c'est ok.

Merci  à vous deux d'avoir répondu.
Mais j'ai encore quelques interrogations.

Je ne comprends votre débat sur x(t) car au final vous trouvez bien tous les deux: k*z*t ,non ?

bonsoir,

On a eu des problèmes à comprendre l'énoncé :

Donc d'une part,
"un ballon de vitesse verticale V0 qui est indépendant de l'altitude z"

Si on traduit çà par simplement v_z = V0; => z(t) = V0*t  car z(t=0)=0.

"une vitesse horizontale qui est proportionnelle à l'altitude"

v_x = k*z  car k*z(t=0)=0

Maintenant pour avoir x(t) il faut intégrer par rapport au temps mais v_x(t) = k*z(t).. z dépend du temps.
x(t) = k*V0*t²/2 + const integration
const = 0 car x(t=0) = 0.

Finalement :
x(t) = k*V0*t²/2
z(t) = V0*t


x= k*z²/(2*V0)

---------------
Désolé pour le arctan et le reste, j'avais essayé de voir comment évoluait l'angle du vecteur position au cours du temps pour mieux me représenter
la trajectoire.

Pour le rayon de courbure, calcul sans doute l'accélération normale et à partir de l'effet centrifuge (a_n(t) = v(t)²/R(t)) tu peux en déduire R qui ici dépend du temps.
Vu le caractère parabolique de la trajectoire, ce rayon ne peut que diminuer.

Bonsoir,

Oui, ton énoncé n'était pas très clair...
Je pense qu'il parlait d'un ballon-sonde (montgolfière) et non sur un ballon (style ballon de foot qu'on lance).

Au vu des équations de Magisterien, j'ai finalement deviné qu'il s'agissait d'un ballon-sonde parce que ça ne me paraissait pas logique que z(t) = v0.t, cela signifiait que z(t) était une fonction toujours croissante du temps et que par conséquent, l'altitude augmentait toujours. D'où ma compréhension du ballon qui monte et redescend en mouvement de chute libre et l'intervention de la gravitation...

Mais maintenant que j'ai mieux cerné l'énoncé, je suis donc d'accord avec magisterien et ses équations.



J'avais compris le problème dans ce sens :

Classiquement, on a ça :
Mobile lancé selon un angle avec une certaine vitesse v.
ax = 0
az = (-g) [axe vers le haut]

vx(t) = v.cos() = Cste
vz(t) = (-g).t + v.sin()

D'où le système d'équation paramétrique suivant :
x(t) = v.cos().t
z(t) = (-g.t²)/2 + v.sin().t
(en posant qu'à t = 0, x = 0 et z = 0)

Et de là, on peut en tirer que :
t = x/(v.cos ) => z(x) = (-g.[x/(v.cos )]²/2) + v.sin().(x/(v.cos ))

D'où l'équation de la trajectoire :
z(x) = -g.x²/[2.v.cos²()] + v.tan()
(trajectoire parabolique)



Mais là, j'avais compris ainsi :
ax = "à déterminer"
az = (-g)  (toujours valable, mouvement de chute libre selon l'axe Oz)

vz(t) = (-gt) + v0 = dz(t)/dt [par définition]
vx(t) = kz(t) = dx(t)/dt [par définition]
(proportionnelle à l'altitude, fonction z dépendant du temps t...)

z(t) = vz(t).dt = (-g.t²/2) + v0.t
x(t) = vx(t).dt = kz(t).dt = k[(-g.t²/2) + v0.t].dt = (-kg.t³/6) + k.v0.t²/2  (+0 pour respecter la condition initiale)


D'où mon système d'équation paramétrique :
x(t) = (-kg.t³/6) + v0.t²/2
z(t) = (-g.t²/2) + v0.t

Et de ça, va en tirer l'expression de z(x) !!!


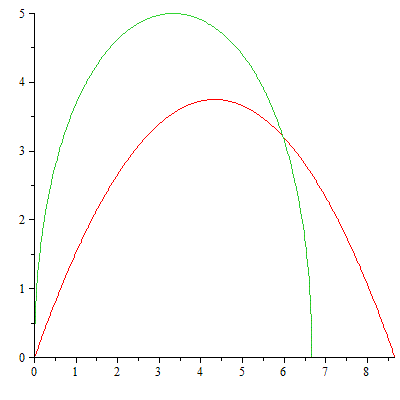
On obtient donc ces deux trajectoires :
En rouge : parabolique classique (v = 10, g = 10, = /3)
En vert : la courbe en "cloche" de mon second raisonnement (v0 = 10, g = 10, k = 1)


Du coup, magisterien et moi n'arrivions pas au résultat k*z*t parce z n'est pas une constante mais une fonction du temps z(t) qui ne s'intègre donc pas z*t mais z(t).dt dans mon cas !


Ceci dit, quel joli problème et débat, simplement pour une simple différence de compréhension d'énoncé... Tu devrais peut-être en faire part à ton prof.
Sûrement n'aura-t-il pas songer à cet aspect-là !