Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

Mécanique 8

Posté par
Flewer47 31-07-16 à 18:02

Bonjour,

Là, on parle d'orbite géostationnaire. Voici l'énoncé :
Une fusée amène un satellite sur une trajectoire circulaire d'altitude h_1=200 km située dans le plan équatorial. On veut transférer le satellite sur une orbite géostationnaire.
A cet effet on donne au satellite un accroissement instantané de vitesse \Delta v_1 qui l'amène sur une orbite elliptique de transfert. Un deuxième accroissement de vitesse \Delta v_2 est alors nécessaire pour le caler sur son orbite géostationnaire.
1) Déterminer le rapport \frac{\Delta v_2}{\Delta v_1}.
Indication : Pour une trajectoire elliptique, l'énergie mécanique est la même que celle d'une trajectoire circulaire dont le demi grand axe a serait le rayon.
2) Faire l'application numérique avec G=6,67\cdot 10^{-11} \cdot kg^{-1} m^{-3}s^{-2}; M_T=6 \cdot 10^{24} kg; R_T=6400 km.
Commenter le résultat
J'ai d'abord compris que a=h_1+h_2 (h_2 étant l'altitude de l'orbite géostationnaire).
Je comprends qu'il faut utiliser la conservation de l'énergie mécanique, mais je ne vois pas comment pour faire apparaître ces accroissements de vitesse..

Posté par
Flewer47re : Mécanique 8 31-07-16 à 18:20

Pardon, 2a=h_1+h-2.

Posté par
Flewer47re : Mécanique 8 31-07-16 à 18:20

Je vais y arriver : 2a=h_1+h_2.

Posté par
vanoisere : Mécanique 8 31-07-16 à 21:04

Je ne suis pas sûr de ton résultat sur a...
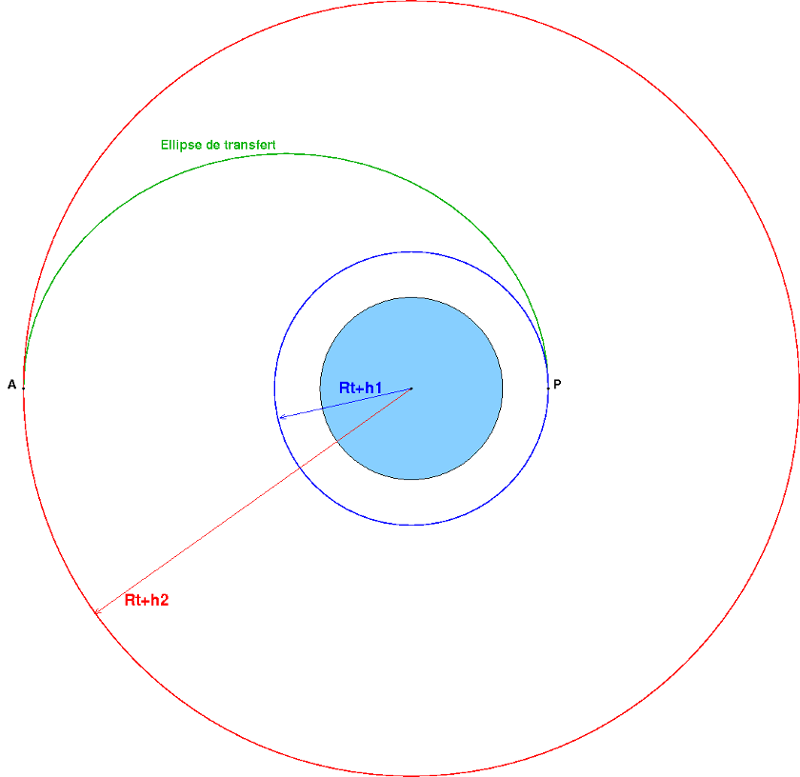
Voici un schéma représentant la demie ellipse de transfert qui devrait t'aider.
Pour les accroissements de vitesses : le résultat est immédiat si tu connais les expressions de la vitesse à l'apogée et au périgée d'une trajectoire elliptique. Sinon, tu peux t'en sortir en raisonnant sur l'accroissement d'énergie mécanique comme suggéré par l'énoncé. Il faut tout de même connaître l'expression générale de l'énergie potentielle gravitationnelle.
Voici une fiche résumant le cours sur les mouvements à forces centrales et le mouvement elliptique. Certaines démos ont disparu du programme de certaines filières de prépa. Cela devrait tout de même t'aider. Il s'agit de la fiche n° 8 que tu trouveras ici :

Mécanique 8

Posté par
Flewer47re : Mécanique 8 31-07-16 à 21:39

Effectivement, j'avais oublié le rayon de la Terre pour a..
On a donc 2a=2R_T+h_1+h_2.

Quelle est l'idée de l'accroissement de l'énergie mécanique ? Et quelle est cette expression générale ? Celle donnée dans la fiche ne semble vraiment pas au programme..

Posté par
vanoisere : Mécanique 8 31-07-16 à 22:18

Certes, tout n'est pas, depuis deux ou trois ans, au programme (les relations de Binet entre autres). En revanche, tu dois absolument connaître l'expression générale de l'énergie potentielle gravitationnelle :

Ep=-\frac{G.M_{T}.m}{r}
avec r : distance du satellite quasi ponctuel au centre de la terre. J'ai fait une démo utilisant le gradient ; il y en a d'autres...
Pour l'énergie mécanique, la démonstration générale est sur la fiche mais ton énoncé demande de la faire comme si le mouvement elliptique était en fait un mouvement circulaire de rayon a.
Tu peux exprimer l'énergie mécanique sur la trajectoire circulaire d'altitude h1, l'énergie mécanique sur la trajectoire de transfert elliptique, l'énergie mécanique sur la trajectoire circulaire d'altitude h2. Les accroissements d'énergies en P et en A sont des accroissements d'énergies cinétiques puisque les augmentations de vitesse sont suffisamment rapides pour qu'on puisse considérer qu'elles se font à altitudes fixes. Facile alors d'obtenir les augmentations de vitesse. La masse m du satellite n'étant pas fournie, tu ne pourras faire l'application numérique que pour le rapport des accroissements...

Posté par
Flewer47re : Mécanique 8 31-07-16 à 22:24

Je connais bien évidemment de cette expression, je pensais que tu parlais d'une encore plus générale, ce qui me semblait un peu louche.

D'accord, je vais travailler sur ça, et je reviens. Merci !

Posté par
Flewer47re : Mécanique 8 31-07-16 à 23:05

J'obtiens, en posant R_i=R_T+h_i :

\frac{\Delta v_2}{\Delta v_1}=\frac{-R_1^2+R_2R_1}{-R_2R_1+R_2^2}.

Cela vous semble-t-il correct ?

Posté par
vanoisere : Mécanique 8 01-08-16 à 15:31

Bonjour
je n'obtiens pas ce rapport. Peux-tu poster les expressions des vitesses que tu obtiens en P et en A avant et après accélération. Cela permettra de savoir s'il y a une erreur de physique ou une simple étourderie de calcul (nullement exclue de ma part d'ailleurs...)
de plus, ton rapport peut encore se simplifier...

Posté par
Flewer47re : Mécanique 8 01-08-16 à 15:56

Effectivement, j'ai oublié de mentionner que j'avais les différences des vitesses au carré ici.
J'ai fait plutôt avec l'énergie mécanique, comme proposé dans l'énoncé.

J'ai dit que :

\frac{\Delta v_2^2}{\Delta v_1^2}=\frac{E_{m,2}-E_{m,a}}{E_{m,a}-E_{m,1}}.

On a E_{m,2}=-\frac{GM_Tm}{2(R_T+h_2)} et de même, E_{m,1}=-\frac{GM_Tm}{2(R_T+h_1)} puis E_{m,a}=-\frac{GM_Tm}{R_T+h_1+h_2}.

Je n'ai donc pas vraiment le bon rapport..

Posté par
vanoisere : Mécanique 8 01-08-16 à 16:47

Aie !
Le rapport des variations d'énergies mécaniques te donne effectivement le rapport des variations d'énergies cinétiques dont aussi le rapport des variations de carrés de vitesses qui n'est bien sûr pas le carré du rapport des variations de vitesses.
\Delta(v_{2}^{2})=v_{2f}^{2}-v_{2i}^{2}\neq\left(\Delta v_{2}\right)^{2}\;si\;\Delta v_{2}=v_{2f}-v_{2i}

Posté par
Flewer47re : Mécanique 8 01-08-16 à 19:39

Je suis bien d'accord, et c'est bien ce que j'ai voulu écrire (j'entendais ça par le fais que je n'avais pas le bon rapport).

Mais comment faire pour ne pas avoir la différence des vitesses au carré ?

Posté par
vanoisere : Mécanique 8 01-08-16 à 23:48

Je vais traiter le cas du point P. Je te laisserai traiter celui du cas A.
Première méthode : elle suppose de connaître l'expression de la vitesse pour un mouvement circulaire de rayon R :

v=\sqrt{\frac{GM_{T}}{R}}
et l'expression de la vitesse sur une trajectoire elliptique de demi grand axe a à la distance r du centre de la terre :
(voir fiche déjà citée dont le contenu n'est plus au programme de toutes les filières prépas...) :

v=\sqrt{GM_{T}\left(\frac{2}{r}-\frac{1}{a}\right)}
Avec tes notations, on obtient en P avant et après accélération :

v_{1i}=\sqrt{\frac{GM_{T}}{R_{1}}}\;;\;v_{1f}=\sqrt{GM_{T}\left(\frac{2}{R_{1}}-\frac{2}{R_{1}+R_{2}}\right)}=\sqrt{GM_{T}\cdot\frac{2R_{2}}{R_{1}\left(R_{1}+R_{2}\right)}}

\triangle v_{1}=\sqrt{\frac{GM_{T}}{R_{1}}}\left(\sqrt{\frac{2R_{2}}{R_{1}+R_{2}}}-1\right)
Seconde méthode : si on ne connais pas l'expression de la vitesse le long d'une trajectoire elliptique, on peut raisonner sur l'énergie. L'étude du mouvement circulaire étant connue, l'expression de v_{1i} est connue ainsi que celle de l'énergie mécanique dans ce cas :

E_{m}=-\frac{GM_{T}m}{2R}
On admet que pour le mouvement elliptique, l'énergie mécanique s'obtient en remplaçant R par a. Ainsi :

\frac{1}{2}m\left(v_{1f}^{2}-v_{1i}^{2}\right)=E_{m1f}-E_{m1i}=-\frac{GM_{T}m}{2}\left(\frac{2}{R_{1}+R_{2}}-\frac{1}{R_{1}}\right)=\frac{GM_{T}m}{2}\left(\frac{R_{2}-R_{1}}{R_{1}\left(R_{1}+R_{2}\right)}\right)

v_{1f}^{2}=\frac{GM_{T}}{R_{1}}+\frac{GM_{T}}{R_{1}}\cdot\frac{R_{2}-R_{1}}{R_{1}+R_{2}}=\frac{GM_{T}}{R_{1}}\cdot\left(1+\frac{R_{2}-R_{1}}{R_{1}+R_{2}}\right)=GM_{T}\cdot\frac{2R_{2}}{R_{1}\left(R_{1}+R_{2}\right)}
Les deux méthodes conduisent heureusement au même résultat ! Je te laisse traiter le cas du point A. L'expression littérale du rapport des deux variations de vitesses est assez laborieuse... Il serait intéressant aussi de déterminer les deux augmentations relatives de vitesses :

\frac{\triangle v_{1}}{v_{1i}}\quad et\quad\frac{\triangle v_{2}}{v_{2i}}

Posté par
Flewer47re : Mécanique 8 02-08-16 à 11:22

Merci, j'ai compris comment  il fallait faire.

Je trouve \frac{\Delta v_2}{\Delta v_1}=\frac{\sqrt{R_1}}{\sqrt{R_2}}}(\frac{\sqrt{R_1+R_2}-\sqrt{2R_1}}{\sqrt{2R_2}-\sqrt{R_1+R_2}}).

On a aussi :
\frac{\Delta v_{1}}{v_{1i}}=\frac{\sqrt{2R_2}-\sqrt{R_1+R_2}}{\sqrt{R_1+R_2}}\quad et\quad\frac{\Delta v_{2}}{v_{2i}}=\frac{\sqrt{R_1+R_2}-\sqrt{2R_1}}{\sqrt{2R_1}}.

Les applications numériques (arrondies) donnent, pour h_2=36000  km :
\frac{\Delta v_2}{\Delta v_1}= 0,6 \\ \frac{\Delta v_{1}}{v_{1i}}= 0.00138 \\ \frac{\Delta v_{2}}{v_{2i}}= 0.927.

Sauf erreur bien entendu.

Posté par
vanoisere : Mécanique 8 02-08-16 à 12:09

Bonjour
D'accord avec toi pour les calculs littéraux. Je n'ai pas vérifié les applications numériques.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !