Inscription / Connexion Nouveau Sujet
Mécanique 6
Bonjour,
Voici un nouvel exercice :
On considère un point matériel , de masse
, que l'on lâche sans vitesse initiale sur un boulier hélicoïdal d'axe
.
La trajectoire de est
.
On suppose qu'il n'y a pas de frottements.
1) Calculer le temps mis par pour aller de
à
. On donne
.
2) Calculer la réaction du support sur
.
Pour la 1), je n'ai pas eu besoin d'utiliser la valeur de l'intégrale : la conservation de l'énergie mécanique puis une double intégration permet d'obtenir , puis
. Je trouve
.
Je voudrais bien savoir quelle méthode est nécessaire pour utiliser l'intégrale donnée.
Pour la 2), s'il n'y a pas de frottements, la réaction du support est selon si on passe en polaire. Je voudrais bien utiliser la RFD, mais je n'arrive pas à projeter correctement..
La méthode avec l'intégrale est très certainement due à une séparation des variables après avoir travailler en polaire.
Pour la 2), j'ai du mal à paramétrer la chose..
Bonjour
J'ai travaillé en coordonnées cylindro-polaires (ou cylindrique) en utilisant la base locale (Ur,U ,Uz). Le théorème de l'énergie-puissance conduit effectivement à
,Uz). Le théorème de l'énergie-puissance conduit effectivement à et
. Par intégration j'obtiens la même chose que toi. Je ne comprends pas l'intérêt pour ces questions de l'intégrale fournie ; mais parfois : les exos ne sont que des extraits de problèmes plus longs. Cette intégrale était peut-être utile dans d'autres questions...
En absence de frottement, la puissance instantanée de la réaction de vecteur F est nulle à chaque instant, ce qui se traduit par : , ce qui te donne la direction du vecteur force.
Il te faut ensuite projeter la RFD suivant Ur en coordonnées cylindro-polaires ; puisque tu connais ...
La réaction du support est bien selon .
J'ai juste du mal à projeter, j'ai du mal à me le représenter..
Je vais essayer encore..
En coordonnées cylindro-polaires, dans le cas particulier r =R : constante :
La puissance de la réaction étant identiquement nulle :
De plus :
Par dérivation on obtient le vecteur accélération de M :
Je te laisse terminer... Voici un schéma illustrant les coordonnées cylindro-polaires dans le cas d'une source de champ à symétrie axiale. Tu peux facilement l'adapter à la situation de l'exercice.
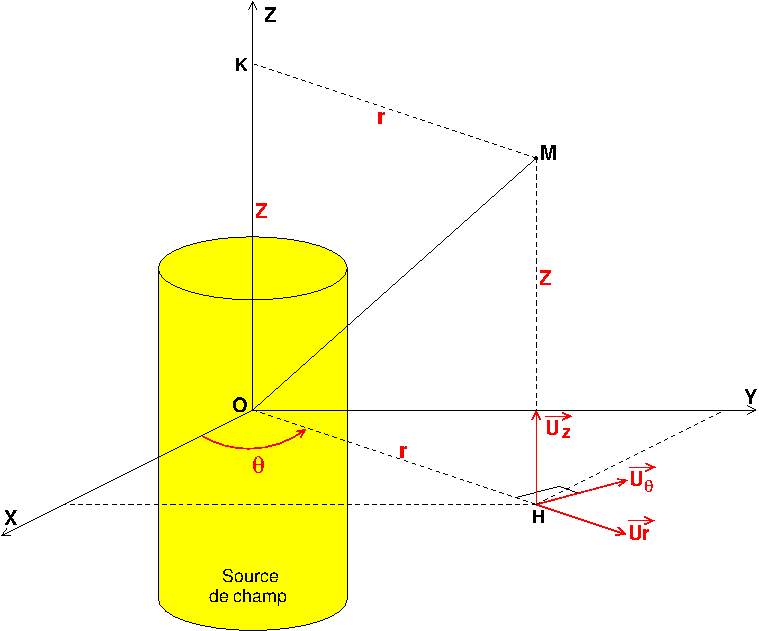
Je me compliquais la vie sur mon schéma en fait. Voilà pourquoi il est important de faire un schéma clair et précis !
Merci de ton aide !


