Inscription / Connexion Nouveau Sujet
Mécanique
Bonsoir,
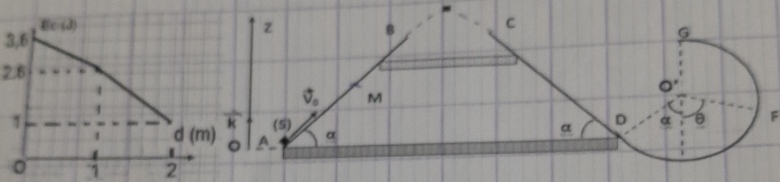
Exercice : la figure ci-dessous représente trois rails guidant un corps (S) de masse m=0,2 kg, pendant son mouvement,
AB rectiligne de longueur L=2m, et incliné d'un angle 
=30° par rapport à l'horizontal,
-CD de même longueur et de même angle d'inclinaison,
-DFG circulaire de rayon r=20 cm et de centre O';
Le corps (S) est lancé du point A avec une vitesse V0 suivant la direction (AB).
L'étude de son mouvement par les moyens appropriés a permis la représentation des variations de énergie cinétique en fonction de la distance parcourue lors de la première étape. (voir graphe).
*** Le problème sera traité sans application du T.E.C. On prend g=10m.s-2 et Epp(O)=0 J,
1. Calculer Epp(B) et Epp(M). (M est le milieu de AB ),
2. En exploitant le graphe , calculer Em(A), Em(M) puis Em[sub](B).
3. Conclure.
4. Déterminer l'intensité de la force de frottement.
5. Le corps (S) quitte la piste au point B et arrive au point C après une chute parabolique dans l'air.
Tous les frottements sont négligeables dans la suite du problème.
5.1. Montrer que E[sub]c(C)= Ec(B).
5.2. Exprimer Epp(F) en fonction de m, g, r, et 
.
5.3. L'étude dynamique du mouvement de (S) montre que l'intensité de la réaction R au point F s'écrit sous la forme :
- Trouver l'expression de R en fonction de r, g, m, , , L et vc (la vitesse de (S) au point C),
5.4. Est-ce-que le corps (S) atteindra le point G ? Justifier la réponse.
Réponse :
1. Epp(B)= m.g.ZB=m.g.L.sin(30)=0,2J
Epp(M)=0,1J.
2. Em(A)= Ec(A)+Epp(A)=3,6+0=3,6J
Em(M)=2,7J.
Em(B)=0,2+2=2,2J
3. la valeur de l'énergie mécanique n'est pas constante au cours de cette étape.
donc le système en mouvement sur le plan incliné est dissipatif.
4. Em(B) -Em(A)=-1,4 J
et Em(B)- Em(A)=w(vec f)
d'où f=0,7N.
5
5.1. Absence de frottement et le travail du poids p est conservatif donc : Em(B)= E m(C)
Ec(B)+Epp(B)=Ec(C)+Epp(C) or Epp(B)=Epp(C) (d'après les données: B et C ont des cotes égales ) .
donc Ec(B)=Ec(C).
5.2. Epp(F)= m.g.zF et zF= r.cos -r cos ,
Donc : Epp(F)=m.g.r.(cos -cos ),
5.3. et 5.4. je n'ai pas trouvé la solution à la question 5.3.
Merci de me débloquer et corriger.
Bonjour,
Commence par vérifier tes réponses à la question 1
Epp(B)= m.g.ZB=m.g.L.sin(30°) = ...
Epp(M)=...
Et après corrige la suite en conséquence.
Bonjour
et merci au temps pour moi.
Je n'ai pas multiplié par g pour le calcul Epp(B).
Donc Epp(B)=2J et Epp(M)=1.
2. Em(A)=3,6J ; Em(M)=3,6J; Em(B)=3J
3. Il n'y a pas conservation de l'énergie mécanique entre le point M et B.
4. Em(B)-Em(M) =3-3,6=-0,6 J
Donc intensité des frottements f=0,3N.
Voilà pour cette partie .
Pardon.
Bonjour,
"Donc intensité des frottements f=0,3N."
Cela mériterait des explications.
L'intensité des frottements n'est pas la même sur AM que sur MB
5.3
L'énoncé précise qu'il n'y a plus de frottement à partir du point B --> l'énergie mécanique est conservée partout après le point B ...
Donc Eméc(F) = Eméc(B) = Eméc(C) (= 3 J)
On sait aussi que Eméc(C) = 1/2*m.(V(C))² + m*g*L.sin(alpha)
--> Eméc(F) = 1/2*m.(V(C))² + m*g*L.sin(alpha)
----
Or Eméc(F) = Epp(F) + Ecin(F)
comme tu as calculé Epp(F) = mgr(cos(alpha) - cos(theta)), il vient :
1/2*m.(V(C))² + m*g*L.sin(alpha) = mgr(cos(alpha) - cos(theta)) + Ecin(F)
Or Ecin(F) = (1/2).m.V(F)²
1/2*m.(V(C))² + m*g*L.sin(alpha) = mgr(cos(alpha) - cos(theta)) + E(1/2).m.V(F)²
Tu peux en tirer l'expression de (V(F))² en fonction de m,g,r,alpha,theta, L et V(C) et en déduire l'expression de R
Bonjour,
Pour la question qui suit 5.3 .
C'est purement mathématique :
J'ai toujours considéré les frottements absents après B comme mentionné et après traitement j'ai trouvé pour que (S) atteint le point G il faut que
.
Or quand on remplace la quantité entre parenthèses par les valeurs de chaque paramètre , donne un résultat négatif ce qui est impossible pour une grandeur au carré qui est toujours positif.
Merci encore.
Bonjour,
Au point 5.3, on te demande d'exprimer R en fonction de m,g,r,alpha et theta, L et Vc
... ce n'est pas ce que tu as fait.
Pour y arriver, c'est effectivement uniquement calculatoire, il suffit de suivre ce que j'ai indiqué dans mon message précédent.
Tu dois donc trouver R = ... (une fonction dépendant de m,g,r,alpha et theta, L et Vc)
Si le R trouvé est > 0 ... le mobile peut atteindre le point F et aller plus loin
Si le R trouvé est = 0 ... le mobile peut atteindre le point F ... et là, il tombe hors de la piste
Si le R trouvé est < 0 ... le mobile ne peut pas atteindre le point F , il est tombé de la piste avant d'atteindre le point F.
Si tu ne fais pas d'erreur, tu vas trouver une formule R = ... et en remplaçant m,g,r,alpha et theta, L et Vc par leurs valeurs numériques, tu vas trouver que R > 0 (au point F), donc le mobile peut atteindre et dépasser le point F.
-------------
Pour le 5.4, c'est comme pour le 5.3, MAIS en modifiant ce qu'il faut dans les formules pour calculer la valeur de R au point G et plus au point F.
Donc R = m.(V(G))²/r + m.g.cos(Pi) (car pour atteindre le point G, theta vaut alors Pi)
En reprenant la formule finale de R que tu aurais du trouver au point 5.3, on trouve aisément celle nécessaire au point 5.4.
Rien ne change ... si ce n'est la valeur de l'angle theta (qui ici vaudra 180° (Pi))
Il suffira de calculer numériquement cette nouvelle valeur de R (pour le point G) et :
Si le R trouvé est >= 0 ... le mobile peut atteindre le point G.
Tu devrais trouver que c'est le cas.
Pardon .
Merci j'ai répondu à cette question c'est bon.
La preuve c'est que j'ai trouvé le résultat suivant :
.
Et j'ai procédé par l'égalité de l'énergie mécanique en en F et en G ( par hypothèse) puis je tire vc 2 comment indiqué dans le post précédent et j'ai trouvé un résultat impossible et donc on ne peut atteindre G.
Bonjour,
Bon, tu as trouvé l'expression de R, soit R = m/r.(V(C))² + m*g*[2L/r.sin(alpha) - 2.cos(alpha) - cos(theta)]
En supposant qu'il n'y a pas d'erreur ...
Si tu calcules la valeur numérique de R (pour le point F), on a :
On sait que Emec(C) = (1/2).m.V(C))² + m*g*L.sin(alpha) = 3 Joules
--> m/r.(V(C))² + m*g*2L/r.sin(alpha) = 2*Emec(C)/r = 2*3/0,2 = 30
--> R = 30 - mg*(2.cos(alpha) + cos(theta))
R = 30 - 2*(2.cos(30°) + cos(60°)) = 25,53 N
R > 0 et donc le mobile dépassera le point F.
(calculs non vérifiés)
-----------
Pour la 5.4
On adapte la formule de R par : R = m.(V(G))²/r + m.g.cos(theta) (ici theta = 180°)
Et on fait un raisonnement analogue au point précédent.
Annuler
connectez vous