Inscription / Connexion Nouveau Sujet
Mécanique 3
Bonjour,
Voici tout d'abord l'énoncé de mon exercice :
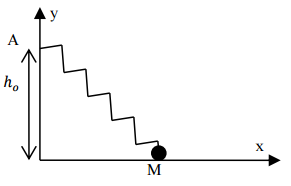
Le point M de masse m est astreint à se déplacer sans frottements sur l'axe horizontal Ox. La longueur du ressort à vide est (avec
).
1) Etudier l'équilibre de M (positions, stabilité).
2) Etudier le mouvement de M au voisinage d'une position d'équilibre stable.
Cela peut paraître idiot, mais je n'arrive pas à projeter la force de rappel sur l'axe horizontal afin d'étudier par la suite le signe de pour connaître par la suite les positions d'équilibre (en étudiant le signe).
Bonjour
Je ne pense pas que la technique consistant à projeter sur deux axes les vecteurs force soit la meilleure ; elle ne permettra pas simplement d'étudier la nature des équilibres. Le mieux est d'établir l'expression de l'énergie potentielle. A un équilibre correspond un extremum de Ep ; si cet extremum est un maximum, l'équilibre est instable , si cet extremum est un minimum, l'équilibre est stable.
L'énergie potentielle élastique à pour expression : Ep=½ .k.(L-Lo)2
L'énergie potentielle de pesanteur restant constante peut être choisie nulle. Tu n'as plus qu'à exprimer (L-Lo)2 en fonction de x , de hoet de Lo...
On a .
On en déduit que .
La condition d'équilibre impose alors 3 positions : .
Pour savoir si chacune des positions est un maximum ou un minimum local pour l'énergie potentielle, on dérive encore une fois pour étudier le signe :
.
On en déduit que est une position d'équilibre instable et que les deux autres sont stables, tout ça car
. Est-ce exact ?
Pour la deuxième question, je suppose qu'il va falloir faire un développement limité en u si on pose . Mais encore une fois, je ne vois pas par où commencer pour le faire..
En fait j'utilise le principe fondamental de la dynamique, et j'obtiens un mouvement sinusoïdal de période .
Non en fait, je me suis trompé.
J'ai :
.
En faisant un DL à l'ordre 1 :
Donc un mouvement sinusoïdal de période .
Est-ce exact ?
Dans ta projection de la force sur l'axe des x, as-tu tenu compte du cosinus de l'angle entre le ressort et l'axe des x qui vaut x/(l-lo) ? Je crois que oui car ta réponse de 18h27 me parait correcte.
Sinon, tu peux aussi écrire l'expression de l'énergie mécanique Em= Ec+Ep et dériver par rapport au temps : dEm/dt = 0 
t en négligeant les frottements. En divisant tous les termes de l'équation obtenue par la vitesse, tu obtiens l'équation différentielle recherchée et, selon mon calcul, tu obtiens ta réponse de 18h27... Peut-être un peu plus rapide dans la mesure où tu as déjà calculé dEp/dx...
En fait, j'ai fais ta deuxième méthode pour y arriver, mais je ne semble pas y arriver par le principe fondamental et la projection sur l'axe des x...
Annuler
connectez vous