Bonjour,
Pour un mouvement circulaire uniforme, il existe une relation entre le rayon de la trajectoire, la vitesse angulaire et l'accélération.

Bonsoir à tous...
J'imagine que "vélocité angulaire" veut dire "vitesse angulaire".
Dans ce cas:
a_n=v²/R
Et V=R, dois-je faire intervenir aussi l'accélération tangentielle?
Je tire des premières expressions:
=(a_n/R)
Mais avec ça je ne trouve pas de reponses justes.
Me suis-je tromper?

Bonsoir,

=(a_n/R)
est une expression correcte.

Si tu veux plus d'aide, il te faut poster ton énoncé dans son intégralité.

Il faudrait un énoncé dont on est certain.

Mais de toute manière, il y a un piège.

La corde a beau avoir 5 m, cela ne signifie par du tout que le rayon de giration est de 5 m.

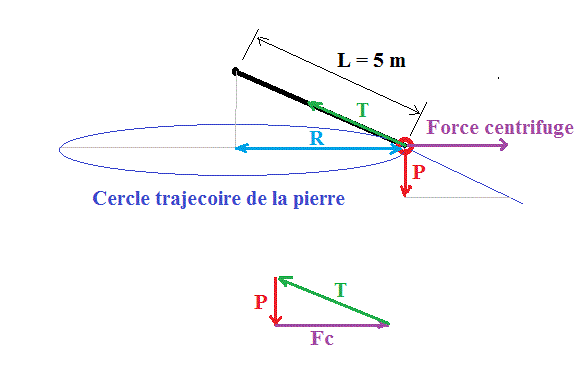
En effet, dans un référentiel lié à la pierre, il y a 3 forces agissant sur la pierre, son poids (vertical vers le bas) et la force centrifuge (horizontale vers l'extérieur), la composante de ces 2 forces est oblique et compensée par la tension du fil.

Donc le fil est oblique (pas horizontal) et la pierre tourne sur un cercle horizontal mais le rayon de ce cercle est < 5 m

Si a est l'accérération centripète, je trouve que le rayon de giration est :

R = L * a/RCarrée(a² + g²) (avec L la longueur de la corde)

a = w².R

w² = a/R

w² = (RCarrée(a² + g²))/L

w = RCarrée[(RCarrée(a² + g²))/L]

Rien vérifié.  

Bonjour J-P, l'énoncé de l'exercice est complet.
Par ailleurs je ne comprend pas pourquoi tu dis que le rayon du cercle est inférieur à la longueur de la corde. Je pensais pourtant que R=L=5m

OK  ?

Ok