Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau licence
Partager :

mecanique

Posté par
mirlamber 14-02-10 à 18:31

bonjour

je dois déterminer le vecteur rotation (1/Ro)
c'est a dire le vecteur rotation de la pièce 1 par rapport au repère Ro

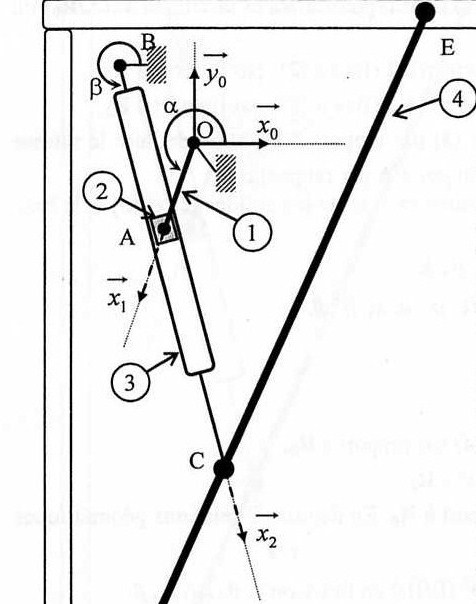
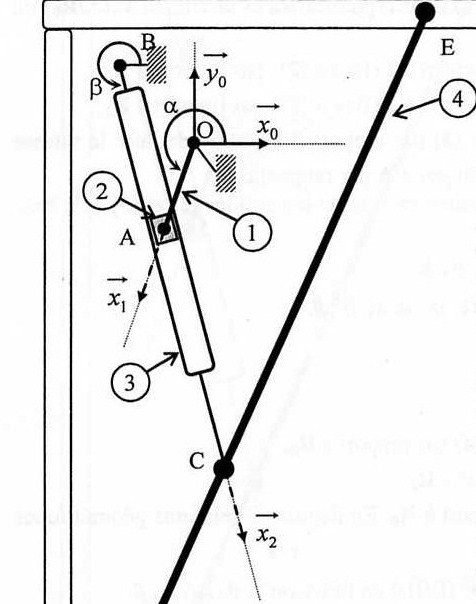
si vous pouviez m'indiquer la formule cela serait vraiment gentil merci d'avance voici la figure

mecanique

Posté par
gbm Webmasterre : mecanique 14-02-10 à 18:37

Salut, d'après ton schéma,

3$\vec{\Omega(1/Ro)} = \frac{d \alpha}{dt}.\vec{zo}

(rotation autour de \vec{zo}, repérée par \alpha)

Posté par
gbm Webmasterre : mecanique 14-02-10 à 18:38

\alpha pour "alpha"

Posté par
mirlamberre : mecanique 14-02-10 à 18:45

tu peux m'expliquer comment tu as trouvé ça parce que dans un exercice similaire j'ai aussi écrit ce résultat mais dans mon cour il y a comme une formule alors je sais pas si je dois le marquer comme ça ou bien utiliser la formule

la formule est = 1/2 (x^d(x)/dt + y^d(y)/dt + z^d(z)/dt)

Posté par
donaldosre : mecanique 14-02-10 à 19:59

La formule générale de ton cours se simplifie pour donner la formule indiquée par gbm dès que l'on a une rotation autour d'un axe repérée par un seul angle.

Je ne pense pas que tu sois tenu(e) de démontrer ce résultat quand tu souhaites l'utiliser.

Posté par
mirlamberre : mecanique 15-02-10 à 12:30

ok merci beaucoup

maintenant je dois calculer la vitesse V(A/Ro)

voila ce que j'ai fait

OA = R x1 par donnée  (vecteur x1)

V(A/Ro) = d(OA)/dt = R*d(x1)/dt

x1 = -sin()xo + cos()yo

donc V(A/Ro) = R*d(x1)/dt = -R*d()/dt * (sin()xo + cos()yo)

je pense avoir juste

c'est pour la question suivante que je bloque :
déterminer la vitesse V(A2/Ro) du point A appartenant à 2 (fixé à(2)) par rapport à Ro

en fait je ne vois pas la différence avec la question précédente

merci d'avance

Posté par
mirlamberre : mecanique 15-02-10 à 15:36

je n'ai toujours pas trouvé et j'ai vraiment besoin d'aide

J'en suis arrivé à dire que

V(A/Ro) = V(A2/Ro)

est ce que c'est juste?

Posté par
gbm Webmasterre : mecanique 15-02-10 à 16:17

Citation :
OA = R.x1 par donnée

V(A/Ro) = d(OA)/dt = R*d(x1)/dt


Juste ici, je suis d'accord.

Citation :
x1 = -sin()xo + cos()yo

donc V(A/Ro) = R*d(x1)/dt = -R*d()/dt * (sin()xo + cos()yo)


NON! On ne projette pas le vecteur x1 ! Utilise le th de changement de base de dérivation

Posté par
mirlamberre : mecanique 15-02-10 à 17:15

merci mais je ne vois pas du tout ce que c'est le théorème de changement de base de dérivation

et je me suis trompé dans ma projection
x1 = sin()yo + cos()xo

j'ai un autre problème si j'utilise la formule = ^OA
je trouve pas pareil que si je fais la dérivée du vecteur OA pour obtenir la vitesse

qu'est ce qui cloche je commence a désespérer ça fait depuis le début de l'aprem que je me bas avec la première question de mon devoir maison

merci beaucoup gbm

Posté par
mirlamberre : mecanique 15-02-10 à 17:26

je crois que je n'arrive pas a projeter x1 si vous pouviez me dire le résultat de cette projection ce serait gentil

merci d'avance

Posté par
gbm Webmasterre : mecanique 15-02-10 à 17:56

Théorème de changement de base de dérivation :

(\frac{d\vec{x1}}{dt})_{Ro}= \vec{\Omega(1/Ro)}\vec{x1}

Posté par
mirlamberre : mecanique 15-02-10 à 18:00

ah d'accord

mais ça ne change rien parce qu'on a
V(A/Ro) = R.d(x1)/dt = R.^x1 = R.d()/dt.zo^x1

il faut bien que j'écrive x1 dans la base xo,yo,zo pour faire le produit vectoriel

Posté par
gbm Webmasterre : mecanique 15-02-10 à 18:47

Citation :
il faut bien que j'écrive x1 dans la base xo,yo,zo pour faire le produit vectoriel


oui sauf qu'écrire x1 = cos(a)xo + .... est bcp plus long que d'utiliszr ce th.

Donc

v(A/Ro) = R.dalpha/dt.y1

Posté par
mirlamberre : mecanique 15-02-10 à 19:01

ok je crois que j'ai compris

maintenant c'est pour déterminer la vitesse V(A2/Ro) du point A appartenant à 2 (fixé à(2)) par rapport à Ro

sachant que le solide 2 est lié au point A et peut tourner autour de ce point. Il peut également se translater suivant x2 dans la glissière du solide 3

Je ne comprend pas parce que pour calculer v(A/Ro) on utilisait le vecteur x1 mais maintenant on utilise quel vecteur???

Je suis perdu
merci

Posté par
mirlamberre : mecanique 15-02-10 à 19:03

et le produit vectoriel de zo^x1 ça ne fait pas -y1 ?

parce que du coup on aurrai v(A/Ro) = -R.dalpha/dt.y1

Posté par
mirlamberre : mecanique 15-02-10 à 20:00

non apres avoir reussi ma projection je trouve bien v(A/Ro) = R.dalpha/dt.y1

est que tu vous pouvais m'aider pour la suite s'il vous plait

Posté par
gbm Webmasterre : mecanique 15-02-10 à 21:09

Pour le moment ce que tu as fait est correct.

Où sont les autres questions ?

Posté par
mirlamberre : mecanique 16-02-10 à 10:55

bonjour

maintenant c'est pour déterminer la vitesse V(A2/Ro) du point A appartenant à 2 (fixé à(2)) par rapport à Ro
sachant que le solide 2 est lié au point A et peut tourner autour de ce point. Il peut également se translater suivant x2 dans la glissière du solide 3

Je ne comprend pas parce que pour calculer v(A/Ro) on utilisait le vecteur x1 mais maintenant on utilise quel vecteur???

et en fait je ne comprend pour pour V(A/Ro)

parce que (1/Ro)^R.x1 = R.d()/dt.zo^(cos().xo+sin().yo)

= - R.d()/dt.(cos().yo+sin().xo)

alors que si je fait la dérivé du vecteur OA j'obtient
d(OA)/dt = R.d(x1)/dt = R.d(cos().xo+sin().yo)
= R.d()/dt.(cos().xo-sin()yo) = R.dalpha/dt.y1

pourquoi ça ne donne pas le meme résultat ?

merci d'avance

Posté par
mirlamberdevoir maison porte de garage 17-02-10 à 10:21

bonjour

voici les données

soit Ro (O,xo,yo,zo) le repère fixe du système

le solide 1 possède un mouvement de rotation uniforme autour du point O. La base R1 (O,x1,y1,z1) est liés à ce solide tel que = (xo,x1)

Le solide 2 est lié au solide 1 au point A et peut tourner autour de ce point. Il peut également se translater suivant x2 dans la glissière du solide 3.

Le solide 3 est composé de la glissière et de la barre BC. Il et en mouvement de rotation autour du point B. La base R2 (B,x2,y2,z2) est lié ç ce solide tel que = (xo,x2)

La figure est ci dessous

première question : déterminer la vitesse V(A2/Ro) du point A appartenant à 2

J'ai marqué que V(A2/Ro) = d(OA)/dt/R1 + (R1/R0)^OA.x1
Je pense avoir faux parce que ça me ramène à l'expression de V(A1/Ro)

voila merci de toute aide j'en ai vraiment besoin

devoir maison porte de garage

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 10:58

Tu peux peut-être calculer cette vitesse en te basant sur un autre repère...

Quel est le but de l'exercice?

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 11:16

le but de l'exercice est de déterminer la vitesse du solide 4 par rapport à Ro

la premiere question on demande de trouver V(A/Ro)

j'ai fait V(A/Ro) = d(OA)/dt = R.d(x1)/dt = R.d(cos().xo+sin()yo)
V(A/Ro) = R.d()/dt.(-sin().xo+cos()yo)

maintenant on me demande de trouver V(A2/Ro) pour moi les deux vitesses sont égales

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 11:57

Même si les deux points ont le même mouvement dans {\mathcal R}_0, rien ne t'empêche d'utiliser la formule de dérivation par rapport à un repère différent de {\mathcal R}_1.

Par exemple:

\vec{V}\left(A\in 2/{\mathcal R}_0\right)=\vec{V}\left(A\in 2/{\mathcal R}_2\right)+\vec{\Omega}\left({\mathcal R}_2/{\mathcal R}_0\right)\wedge\vec{BA}

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 12:04

d'accord mais on me demande calculer la vitesse V(A2/R2) dans la question suivante donc c'est plutôt la que je devrais utiliser cette relation ?

Il n'y a pas un autre moyen de calculer cette fameuse vitesse V(A2/Ro) avec la vitesse V(A/Ro) que l'on a calculé juste avant?

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 12:10

Je pense que l'on perdrait moins de temps si tu nous donnait d'emblée l'ensemble des questions.

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 12:10

dans les données on a BA = x(t).x2

est ce que V(A2/R2) = d(x(t))/dt.x2 ?  car la dérivé de x2 est nulle puisque c'est un vecteur unitaire du repère R2

merci

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 12:12

Oui, bien sûr.

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 12:15

d'accord

1) déterminer le vecteur rotation (1/Ro) de la piece 1 par rapport à Ro et la vitesse V(A/Ro) du point A par rapport à Ro

2) déterminer la vitesse V(A2/Ro) du point A appartenant à 2 par rapport à Ro

3) determiner la vitesse V(A2/R2) du point A appartenant à 2 par rapport à R2

4) déterminer le vecteur rotation du point A appartenant à 3 du pont A par rapport à Ro

5) écrire la relation vectorielle de composition des vitessees en A entre les solides 2 et 3 et la base de référence Ro

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 12:16

pour la question j'ai oublié de marquer qu'il faut n déduire la vitesse V(A3/Ro)
désolé

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 13:21

Le solide 1 étant relié au solide 2 par le point A, la vitesse de A\in 1 est la même que celle de A\in 2.

En revanche, A\in 3 ne coïncide avec A\in 2 et A\in 1 qu'à un instant donné. puisque les différentes liaisons autorisent un déplacement de la pièce 2 par rapport à la pièce 3.

Il ne te reste qu'à calculer \vec{V}\left(A\in 3 /{\mathcal R}_0\right) en te rappelant que A\in 3 est nécessairement fixe dans {\mathcal R}_2.

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 13:36

voila ce que je propose

V(A3/Ro) = V(A2/R2) + (R2/Ro)^BA

V(A3/Ro) = d(x)/dt.x2 + d()/dt.zo^x.x2

V(A3/Ro) = d(x)/dt.x2 + x.d()/dt.y2

c'est juste ?

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 13:52

non je me corrige je pense avoir faux

V(A3/Ro) = V(A2/R2) + (R2/Ro)^OA

V(A3/Ro) = d(x)/dt.x2 + d()/dt.zo^R.x1

V(A3/Ro) = d(x)/dt.x2 + R.d()/dt.y1

c'est juste ?

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 14:00

je pense mettre encore planté

V(A3/Ro) = V(A3/R2) + (R2/Ro)^OA

V(A3/Ro) = 0 + d()/dt.zo^R.x1

V(A3/Ro) =  R.d()/dt.y1

J'espère que c'est la bonne cette fois ci

*** message déplacé ***

Posté par
mirlamberquestion sur une formule 17-02-10 à 14:03

bonjour

est ce que je peux utiliser la formule

V(A/Ro) = V(A/R1) + (R1/R2)^OA

si Ro et R1 non pas une origine commune?

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 15:15

Pas exactement, \vec{V}\left(A\in3/{\mathcal R}_0\right)=\left.\frac{{\rm d}\vec{OA}}{{\rm d}t}\right|_{{\mathcal R}_0} avec A, lié à {\mathcal R}_2.

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 15:16

Comment passe-t-on de cette définition de la vitesse à ta première égalité?

*** message déplacé ***

Posté par
donaldosre : question sur une formule 17-02-10 à 15:17

A ton avis?

Reviens à la définition de la vitesse par rapport à un repère donné...

*** message déplacé ***

Posté par
mirlamberre : question sur une formule 17-02-10 à 15:39

Je pense qu'il faut qu'il faut nécessairement que les repères ai une origine commune mais j'espère me tromper

Sinon bien je ne sais pas du tout

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 15:45

ma première égalité était très similaire sauf que A était lié à Ro du coup je ne vois franchement pas comment m'en sortir puisque je peux pas décomposer car R2 et Ro non pas la même origine

ou alors je projette x2 dans Ro ?

*** message déplacé ***

Posté par
donaldosre : question sur une formule 17-02-10 à 15:53

Comment définit-on la vitesse d'un point A par rapport à un repère {\mathcal R}_O?

*** message déplacé ***

Posté par
mirlamberre : question sur une formule 17-02-10 à 16:01

V(A/Ro) = d(OA)/dt /Ro

c'est ça?

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 16:09

après avoir regardé longuement le dessin et cette phrase de l'énnoncé : Le solide 3 est composé de la glissière et de la barre BC. Il et en mouvement de rotation autour du point B. La base R2 (B,x2,y2,z2) est lié ç ce solide tel que = (xo,x2)

J'en ai déduit que v(A3/Ro) = (R2/Ro)^OA.x1

v(A3/Ro) = d()/dt.zo^OA.x1

v(A3/Ro) = d()/dt.OA.y1

est ce que c'est juste ?

*** message déplacé ***

Posté par
donaldosre : question sur une formule 17-02-10 à 16:28

Oui, et pour arriver à l'expression que tu donnes dans ton premier post, il faut écrire:

\vec{V}\left(A/{\mathcal R}_0\right)=\left.\frac{{\rm d}\vec{OA}}{{\rm d}t}\right|_{{\mathcal R}_0}=\left.\frac{{\rm d}\vec{OA}}{{\rm d}t}\right|_{{\mathcal R}_1}+\vec{\Omega}\left({\mathcal R}_1/{\mathcal R}_0\right)\wedge\vec{OA}

Dès lors ta question de départ devient:

Sous quelle condition l'égalité \left.\frac{{\rm d}\vec{OA}}{{\rm d}t}\right|_{{\mathcal R}_1}=\vec{V}\left(A/{\mathcal R}_1\right) est-elle vérifiée?

Normalement, tu es en mesure de répondre toi-même maintenant...

*** message déplacé ***

Posté par
mirlamberre : question sur une formule 17-02-10 à 16:34

A la condition que O soit l'origine du repère R1 ?

j'ai répondu dans l'autre post mais je dois encore avoir faux je pense

*** message déplacé ***

Posté par
donaldosre : question sur une formule 17-02-10 à 16:55

Oui, c'est ça.

*** message déplacé ***

Posté par
mirlamberre : question sur une formule 17-02-10 à 16:57

pour quelle question j'ai juste pour la réponse à la question de ce topique ou pour ma réponse quant au calcul de V(A3/Ro) dans l'autre topique?

grand merci en tout cas

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 16:58

Tu vas trop vite!

Là encore, pars de la définition de la vitesse du point A (lié au solide 3) et développe, tu verras que tu as commis une erreur et que la formule que tu utilises n'est pas applicable.

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 17:05

v(A3/Ro) = d(OA)/dt /Ro

v(A3/Ro) = d(BA)/dt /R2 + R2/Ro^BA

j'espère vraiment avoir juste cette fois ci

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 17:18

Tu sautes une étape de calcul (qui consiste a décomposer \vec{OA} en \vec{OB}+\vec{BA} et à remarquer que le vecteur \vec{OB} est fixe dans {\mathcal R}_0) mais tu obtiens le bon résultat cette fois.

*** message déplacé ***

Posté par
mirlamberre : devoir maison porte de garage 17-02-10 à 17:27

merci énormément donaldos

pour la question
5) écrire la relation vectorielle de composition des vitesses en A entre les solides 2 et 3 et la base de référence Ro
il faut que je décompose un vecteur pour avoir la décomposition du mouvement puis après je dérive pour avoir la décomposition des vitesses

mais je ne trouve pas quel vecteur décomposer afin de relier le solide 2 et 3?

*** message déplacé ***

Posté par
donaldosre : devoir maison porte de garage 17-02-10 à 17:35

A ce stade, soit tu redémontres la formule de composition des vitesses (je ne t'en empêcherai pas... ), soit tu l'appliques.

Je ne suis pas sûr du résultat qui est attendu dans cette question mais parmi les vitesses que tu as calculé: une correspond à une vitesse d'entraînement, une autre correspond à une vitesse relative donc...

*** message déplacé ***

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !