Inscription / Connexion Nouveau Sujet
Mécanique 12
Bonsoir,
Voici un autre problème :
Une voiture prend une accélération constante . La portière 𝐴𝐵 est restée ouverte, l'angle initial est
. Elle est modélisée par une plaque de hauteur
, de largeur
, de masse
uniformément répartie et de moment d'inertie par rapport à son axe de rotation
. La liaison
est supposée parfaite.
1) Déterminer l'équation différentielle en .
2) En déduire le temps nécessaire à la fermeture de la portière. On donne .
Pour la 2), je sais comment faire, cependant, pour la 1), je veux utiliser le théorème du moment cinétique appliqué à la portière. Mais je trouve une équation différentielle avec du à cause du moment du poids. Et cela ne marche pas ensuite, à cause de l'intégrale donnée qui ne contient pas de
..
Ai-je tort de considérer le poids ici ?
Si l'axe de rotation est vertical, le moment du poids par rapport à cet axe est nul. Je crois que tu as intérêt à raisonner dans le repère non galiléen lié à la voiture, ce qui va te conduire à faire intervenir les pseudos forces d'inertie d'entraînement et de Coriolis....
Pour celle de Coriolis, la situation est particulièrement simple.
Effectivement, évidemment le poids n'intervient pas ici...
Pour la force de Coriolis, comme le référentiel de la voiture n'est pas en rotation uniforme , elle est nulle non ?
Je ne comprends juste pas comment calculer le moment de la force d'inertie ici. Quel vecteur position dois-je considérer, sachant que j'ai l'impression que la force d'inertie est différente selon l'endroit où l'on se trouve sur la portière..
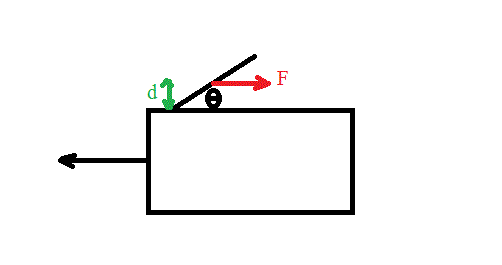
Force inertielle sur la portière: F = m.A (avec m la masse de la portière et A l'accélération de la voiture dans un référentiel terrestre).
Cette force est appliquée au centre d'inertie de la portière, elle est horizontale et dirigée vers l'arrière du véhicule.
F*d = - J.d²theta/dt²
Ceci en négligeant la force aérodynamique sur la portière ...
Sauf distraction. 
Bonjour
Pour la force de Coriolis, comme le référentiel de la voiture n'est pas en rotation uniforme , elle est nulle non ?
La pseudo force d'inertie élémentaire exercée sur une masse élémentaire
d
de volume élémentaire d s'écrit :
où
Quel vecteur position dois-je considérer, sachant que j'ai l'impression que la force d'inertie est différente selon l'endroit où l'on se trouve sur la portière..
La pseudo force d'inertie d'entraînement exercée sur la masse
où
appliquée au centre d'inertie G (c'est la théorie des torseur que tu dois connaître). Évidemment, comme pour le poids, il est faux de dire que G constitue le point d'application de la force même si le moment se calcule comme si...
Dans ce cas, j'ai
L'équation différentielle écrite par JP est correcte sous réserve que le sens positif de rotation et le sens d'orientation de
soient antihoraires, ce qui n'est indiqué nulle part...
Je ne comprends pas comment tu arrives à cette équation différentielle. Quel expression du bras de levier d utilises-tu ?
Remarque 1 : j'utilise volontairement le terme "pseudo force d'inertie" pour bien montrer qu'il ne s'agit pas d'une action exercée par le milieu extérieur sur le système mais d'un terme correctif pour tenir compte du fait que le repère n'est pas galiléen... Le terme "force d'inertie" est cependant encore utilisé.
Remarque 2 : j'espère que la notion de "bras de levier" t'est familière ; sinon tu peux raisonner sur les produits vectoriels où consulté le post que j'ai eu l'occasion de rédiger récemment pour quelqu'un d'autre :
moment d'une force
Remarque 3 : la lettre "a" désigne ici à la fois l'accélération et la demie largeur...
Annuler
connectez vous