Bonjour
Le fusil exercerait quel type de force sur la balle à ton avis?

Euh quand vous dites type de forces c'est conservative / non conservative ?

Non je voudrais savoir la nature de cette force

Le fusil est à au moins 50m de la balle, on va dire, et j'aimerais savoir quelle force peut bien exercer le fusil sur la balle quand elle pénètre dans l arbre

C'est la quantité de mouvement non ?

La force et la quantité de mvt sont deux choses différentes
Ici, la balle ne subit de poussée que dans le canon du fusil mais dès qu' elle en sort il n' y a plus de force exercée par le fusil
Ensuite la balle est soumise à son poids et aux frottements
C'est tout
Ici on assimile la trajectoire de la balle à une droite horizontale (du fait de sa grande vitesse) donc on néglige le poids
Ce qui fait que le mouvement étudier est très simple finalement.

Donc ça veut dire qu'il n'y a aucune force qui s'exerce sur la balle ?
Parce que sinon je pensais à faire t =d/v mais ça me paraît beaucoup trop simple

Non , relis l'énoncé

Mais sur les frottements de l'air on sait rien ni sur l'accélération de la balle ...

On te dit que la balle pénètre dans le bois à t=0
Et y subit une force de freinage constante jusqu 'à ce qu elle s 'arrête

Un petit schéma t 'aidera peut être à mieux comprendre la situation physique dans cet exo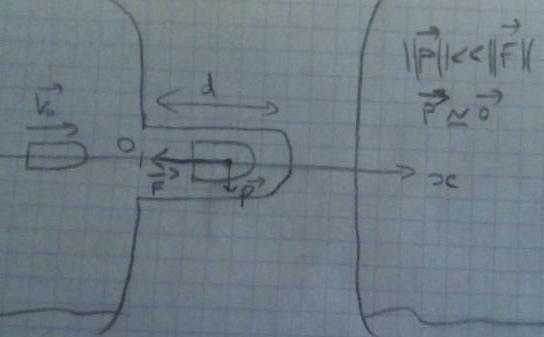



***Image recadrée***

J'ai trouvé 260 ms ...
Donc la variation d'énergie mécanique correspond à la variation d'énergie cinétique car c'est horizontal
Donc delta(Em) = -1/2mv2
= Wab(F)=-F.ab
Donc F=mv2/2d = 17.02N
Or F =mv/t donc t= 260 ms
En fait j'ai pris 15 g pour la balle à peu près

On ne te demande pas d'inventer l'énoncé
Te donne-t-on la masse de la balle?

Non mais ça fait à peu près ça

Si on ne l'a pas donné c'est qu on n'en a pas besoin a priori (sauf oubli dans l'énoncé ce qu est tres rare )
Ici il faut remarquer simplement qu on a un mvt à accélération a constante (à justifier) et donc on en déduit les équations horaires en fct de a, de v0 etc.
En écrivant toutes les conditions à respecter lors du mvt , tu dois trouver la durée demandée normalement

Le mouvement se fait que selon ex donc
a= ax. ex
v= ax t +vo
x(t)=1/2axt2 +vot
On connaît x et vo et ax c'est le coefficient directeur de la pente de v=f(t)
Donc a = -295/t et on remplace dans x(t) ? En tout cas j'obtiens 88 ms ...

1)Avant tout il faut démontrer que l accélération est constante lors du mvt de la balle dans l arbre!

2) et ensuite seulement tu as le droit d'ecrire dans le repère (O,x) de mon dessin:
V = Vo + at avec a<0
X= 1/2 at² + Vo t
en prenant comme conditions initiales
X=0 et v = Vo à t=0

La durée cherchee correspond alors à l instant t1
vérifiant :
V(t1) = 0
X(t1) = d

Ben le fait que la force de freinage soit constante ça le justifie non ?

Oui , mais encore faut il l'expliquer en rédigeant correctement

Je trouve : t1= 2d/Vo

Ça n'a pas un lien avec le fait que la force  exercée par l'arbre sur la balle est égale à celle exercée par la balle sur l'arbre?

Oui je crois que j'ai fait une erreur de conversion
Ça fait 8.8x10-1 s

Ça fait 0,26/295 = ... en s

Pour démontrer que l accélération est constante il faut appliquer le pfd à la balle en négligeant le poids

Si on considère le système = la balle et comme seule force F
On a somme des forces extérieures = m.a ( pour m = cte )
Donc F= m.a et en projetant on a
-F= m.a et donc a =-F/m = cte

En toute rigueur il faudrait plutot dire que la balle est soumise à 3 forces
La force de frottement horizontale F constante
Le poids
La réaction normale
Et en projection sur Ox il ne reste que F donc a_x est constante

Ok d'accord je crois que j'ai finalement compris l'idée de cet exo
Merci pour votre aide et votre temps passé sur l'exo!

De rien
Si tu calcules F avec m=15g tu verras que le poids est totalement négligeable