Inscription / Connexion Nouveau Sujet
Masse volumique atmosphère compressible
Bonjour à tous les mordus de physique,
j'ai un problème concernant la masse volumique de l'air dans l'atmosphère. On suppose l'atmosphère isotherme à T.
Si on considère l'atmosphère comme un fluide COMPRESSIBLE, alors 
varie avec l'altitude. Ok.
Seulement, avec la relation de la statique dP(z)/dz = -gz et l'équation des gaz parfaits P(z)V(z) = n(z)RT on a : comme (z)=m(z)/V(z)
(déjà m(z) et V(z) représentent quoi ? Les masse et volume d'air au-dessus de l'altitude z ?)
=> P(z)M/RT=(z)=> p(z) = RT(z)/M
On injecte cette expression de P(z) dans la relation statique :
RT/M d((z)) = (z)gz
Puis on résout en intégrant, on obtient une valeur de (z) en fonction d'une exponentielle de z.
LE SOUCI : pourquoi le coefficient de compressibilité isotherme Xt n'intervient pas dans l'expression de la masse volumique ? Ça me paraît bizarre qu'on n'ait pas besoin de lui...
Où est l'erreur ? 
Merci de votre aide !
Bonjour
comme
(z)=m(z)/V(z)
(déjà m(z) et V(z) représentent quoi ? Les masse et volume d'air au-dessus de l'altitude z ?)
Tes notations n(z), V(z)... peuvent effectivement induire en erreurs.
As-tu étudié en cours la différence entre grandeurs intensives et grandeurs extensives ?
Les grandeurs intensives sont des grandeurs indépendantes de la quantité de matière du système ; ce sont des variables d'état locales c'est à dire définies en chaque point du système, comme ici la masse volumique et la pression. Les notations P(z) et
(z) ont donc un sens. En revanche, la masse, le volume sont des grandeurs extensives dépendant de la taille du système choisi. Elles ne se mesurent pas en un point : les notations V(z) et m(z) n'ont donc pas de sens...
Pour définir
, tu imagines un récipient de volume V dont les dimensions sont suffisamment petites pour que le gaz puisse y être assimilé à un système homogène et tu utilises l'équation d'état. Cela est parfaitement licite dans ce contexte puisque les grandeurs intensives varient faiblement en fonction de l'altitude.
Tu connais l'expression de
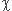T pour un gaz parfait ? Tu es sûr que la pression n'intervient pas ici ???
Au fait : c'est bien toi qui avais sollicité de l'aide à propos du tonneau de Pascal ? Tu as abandonné un peu vite ; des phrases comme "la magnitude de la force" n'incitaient pas à l'optimisme...
Non je n'ai pas abandonné le tonneau de Pascal, je travaille sur plusieurs sujets en même temps; je n'y suis juste pas encore retourné.
Désolée pour le terme "magnitude de la force" c'est juste qu'en anglais on dit "the magnitude" pour parler de l'amplitude. Mon cours est en anglais, d'où l'erreur.
Merci pour ta réponse,
j'ai bien compris la différence entre intensive et extensive.
J'ai bien compris ton ton condescendant aussi.
Annuler
connectez vous