Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Manomètre incliné

Posté par
azer44170 23-02-20 à 10:52

Bonjour,
J'ai juste un question par rapport à la correction d'un exercice qui est la suivante :
P_r - P = \mu g (Z-Z_r) sin (\alpha)
Je ne comprends pas pourquoi on a   (Z-Z_r) sin (\alpha) car on doit avoir la hauteur de colonne d'eau qu'il y a au-dessus de l'horizontale passant par z_r . Par calcul : Sin \alpha = \frac{Z-Z_r}{L} (L la hauteur de colonne d'eau au-dessus de l'horizontale passant par z_r dans la partie droite) donc on devrait avoir : P_r - P = \mu g (Z-Z_r) / sin (\alpha). Voilà si quelqu'un pouvait m'expliquer. Merci.

Manomètre incliné

Posté par
gts2re : Manomètre incliné 23-02-20 à 11:09

Bonjour,

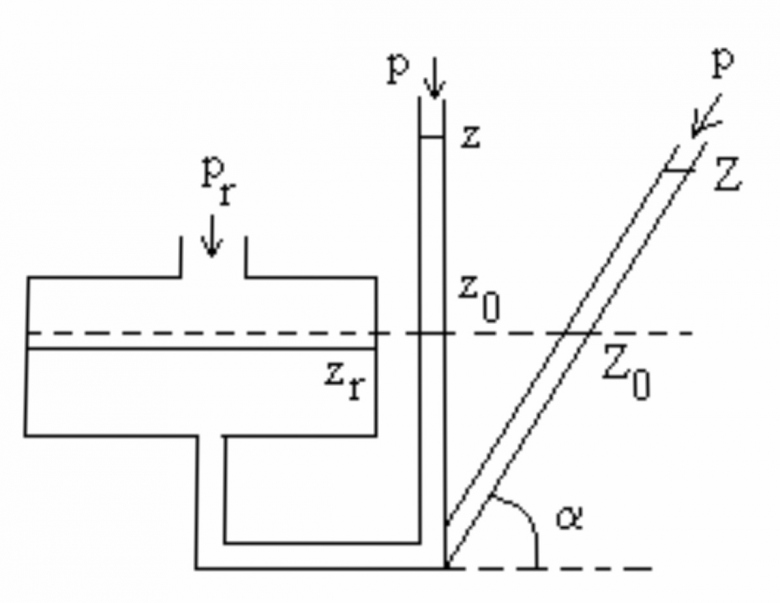
Dans le triangle zZ(pointe en bas), zZ est horizontal, donc l'angle en z est droit.
(z-z0) est bien le côté opposé à

Posté par
gts2re : Manomètre incliné 23-02-20 à 11:13

Bonjour,

Clic intempestif, je continue:
(Z-Z0) sur l'hypoténuse
et donc \sin(\alpha)=\frac{z-z_0}{Z-Z_0}

Posté par
azer44170re : Manomètre incliné 23-02-20 à 12:46

Êtes-vous sûr zZ est horizontal et que l'angle alpha est bien aussi en haut à droite ?

Posté par
gts2re : Manomètre incliné 23-02-20 à 12:57

Bonjour,

Pour zZ horizontal, c'est le "principe des vases communicants" ou dit, de manière plus formelle, l'horizontalité des isobares.

Pour ,  c'est l'égalité d'angle alterne interne

Posté par
azer44170re : Manomètre incliné 23-02-20 à 13:50

Je ne voyais pas comment Z-Z0 pouvait être pouvait être l'hypoténuse puisque c'est une difference de hauteur. Mais d'accord, merci bien !

Posté par
gts2re : Manomètre incliné 23-02-20 à 13:58

Le texte (et le dessin ) n'est pas très clair : il aurait fallu indiquer les axes z (vertical) et Z (selon le tuyau incliné). En fait j'ai interprété le dessin de manière à ce que cela colle avec la correction !

Posté par
azer44170re : Manomètre incliné 23-02-20 à 14:24

En effet, l'exercice est très mal énoncé alors qu'enfaite ce n'était pas compliqué. Merci beaucoup !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !