Inscription / Connexion Nouveau Sujet
mammifère marin
Bonsoir,
J'ai des questions à poser au sujet d'un exercice dont voici l'énoncé :
Un mammifère marin peut être sommairement schématisé par une sphère de muscles de centre O et de rayon R=25 cm dont le métabolisme dégage une puissance thermique volumique  o. L'animal est plongé dans l'eau de conductivité thermique
o. L'animal est plongé dans l'eau de conductivité thermique  e=500 W/m/K. La température très loin du mammifère est supposée égale à To=293K. On se place en écoulement unidimensionnel et permanent. Le vecteur densité volumique de courant d'énergie thermique s'écrit
e=500 W/m/K. La température très loin du mammifère est supposée égale à To=293K. On se place en écoulement unidimensionnel et permanent. Le vecteur densité volumique de courant d'énergie thermique s'écrit où
est un vecteur unitaire radial.
J'ai essayé de faire un bilan et j'ai obtenu :
dQ= Qe-
Qe- Qs+
Qs+ Qc-
Qc- Qd=Pth(r)dt-Pth(r+dr)dt+
Qd=Pth(r)dt-Pth(r+dr)dt+ odrSdt avec Pth la puissance thermique dégagée par le mammifère
odrSdt avec Pth la puissance thermique dégagée par le mammifère
mais dans la correction il y a écrit que l'énergie thermique créée dans le volume pendant une durée dt (soit  Qc) est nulle et je ne comprends pas pourquoi.
Qc) est nulle et je ne comprends pas pourquoi.
Merci d'avance !
Bonsoir
L'énoncé précise que le régime est permanent. Ainsi, le volume d'eau compris entre les sphères de rayon r et de rayon (r+dr) a une température T(r) qui dépend de r mais ne dépend pas du temps. Ce volume d'eau élémentaire ne reçoit donc aucune quantité de chaleur. Cela signifie que la puissance thermique reçue à travers la sphère de rayon r (Pth(r)) est égale à la puissance thermique perdue à travers la sphère de rayon (r+dr) : Pth(r+dr). La puissance thermique Pth est donc la même quel que soit le rayon r de la sphère à travers laquelle on la calcule et vaut  o.V où V désigne le volume du mammifère.
o.V où V désigne le volume du mammifère.
Pour obtenir T(r), il faut appliquer la loi de Fourrier et intégrer. Tu devrais y arriver avec l'aide de ton corrigé !
Attention : l'écoulement est permanent mais pas unidirectionnel : il est radial (à symétrie sphérique si tu préfères).
Ce n'est pas trouver T(r) qui me pose problème mais vraiment comprendre pourquoi l'énergie thermique créée dans le volume pendant une durée dt est nulle. Malgré tes explications, j'ai encore du mal à comprendre. Je vais comparer à un autre exercice que j'ai fait pour que tu puisses trouver une solution pour m'expliquer ce que je ne comprends pas. Dans cet exercice, le cas est similaire (pour moi c'est strictement pareil et c'est justement le problème) mais à l'inverse l'énergie thermique créée dans le volume pendant une durée dt n'est pas nulle.
Voici l'énoncé :
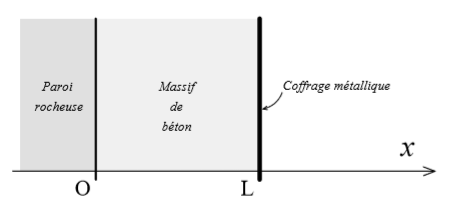
Pour consolider une paroi rocheuse, plane et isotherme, de température To, on coule un massif de béton, de conductivité thermique  . Ce massif est limité de l'autre côté par un coffrage métallique plan, de température uniforme Tc<To. (cf schéma ci-dessous)
. Ce massif est limité de l'autre côté par un coffrage métallique plan, de température uniforme Tc<To. (cf schéma ci-dessous)
Le coffrage est supposé très bon conducteur thermique et sa température est maintenue constante par aspersion d'eau.
La prise du béton correspond à une réaction chimique exothermique.
On note  la puissance volumique de l'énergie thermique dégagée dans la masse du béton, elle est supposée constante. On se place en régime permanent.
la puissance volumique de l'énergie thermique dégagée dans la masse du béton, elle est supposée constante. On se place en régime permanent.
On fait l'hypothèse que la température ne dépend que de la variable d'espace x.
Dans cet exercice il y a écrit dans la correction que l'énergie thermique créée dans le volume pendant une durée dt (soit  Qc) est égale à
Qc) est égale à  Qc=
Qc= dVdt=
dVdt= dxSdt
dxSdt
En fait je ne comprends pas pourquoi dans l'autre exercice on n'a pas la même chose. J'ai l'impression que le cas est vraiment identique alors que non mais je ne comprends pas pourquoi. C'est sans doute ce que tu as essayé de m'expliquer mais je n'ai pas compris. Est-ce que tu pourrais réessayer de m'expliquer s'il-te-plaît ?
Problème sur le mammifère : de l'énergie thermique est créée à l'intérieur du mammifère mais le problème étudie la conduction thermique dans l'eau environnante. Aucun phénomène endo ou exothermique ne se produit dans cette eau. Aucune quantité de chaleur n'est "créée" au sens de ton énoncé.
Le problème du béton est très différent. On étudie la conduction thermique à l'intérieur du béton et l'énoncé précise clairement que chaque volume élémentaire de béton est le siège d'une réaction exothermique. Il y a bien "création" de chaleur dans chaque volume élémentaire de béton.


