Bonsoir,

Je bloque (encore) sur un exercice de physique; toujours de la mécanique mais avec les énergies; voici l'énoncé :

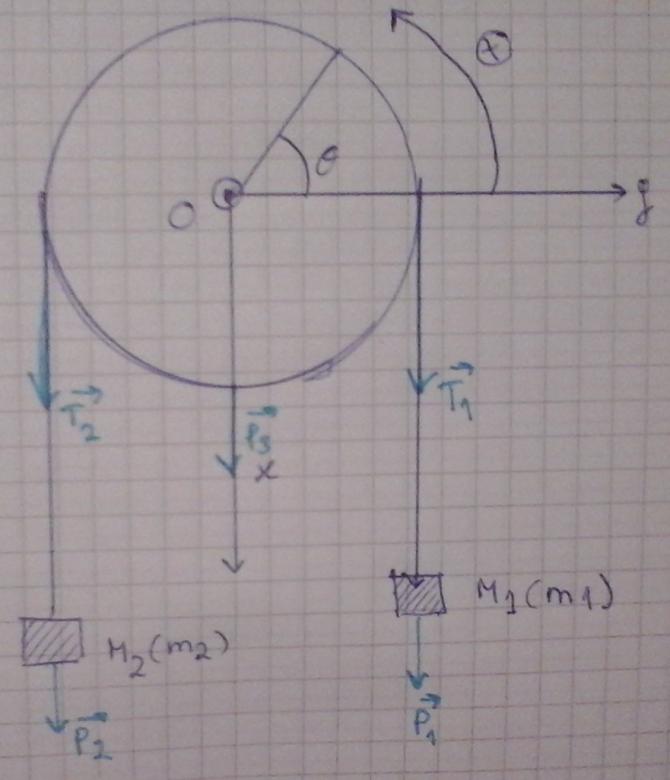
Une poulie de centre 0 et de rayon R et de masse M est mobile, sans frottements, autour d'un axe fixe (Oz) horizontal et normal au plan de la figure. La poulie à un moment d'inertie J par rapport à l'axe de rotation de celle-ci. La composante suivant l'axe (Oz) du moment cinétique de la poulie vaut : Lz= J, avec la vitesse angulaire de la poulie.
Un fil inextensible sans masse ni raideur, passe dans la gorge de la poulie. Nous supposerons que le fil ne glisse pas, par conséquent la poulie tourne lorsque le fil se déplace. 2 objets ponctuels (M1,m1) et (M2,m2) sont fixés à chaque extrémité du fil. Supposons : m2>m1
Au repos les 2 brins du fil pendent verticalement et les 2 objets sont à la même hauteur.
A t=0 on laisse évoluer le système, les 2 objets ont donc un mouvement verticak. L'objet (M1,m1) ralentit donc la chute de l'objet (M2,m2).
Dans la suite, on négligera les frottements du fil sur la poulie.

1) à cause et grâce au fait que le fil ne glisse pas dans la gorge de la poulie, relier la vitesse angulaire à la vitesse de translation des 2 objets. On notera x'1 (resp x'2) la vitesse de M1 (resp M2). On tiendra compte du fait que l'axe (Ox) est vertical descendant.

v=R donc -x'1=R=x'2 <=> =-x'1/R = x'2/R

2) Déterminer la composante suivant (Oz) du moment cinétique total (poulie + les 2 objets) en fonction de  
et de x'2.

Je ne suis pas sur de comprendre la question, il s'agit simplement de calculer le moment cinétique du système poulie + objets ?


3) Par application de la loi du moment cinétique, en déduire une relation entre x''2 et ', moyennant les grandeurs m1,m2,J,R, et g. et 4)En déduire l'expression de x''2 en fonction de grandeurs m1,m2,J,R, et g.


x'1=R

x'1=-x'2
système : fil + poulie + les deux masses
référentiel : terrestre galiléen
BDF : P1, P2, Ppoulie, réaction de l'axe de rotation, T1 ,T2,

Théorème du moment cinétique par rapport à Oz : dLo/dt =Mo
Lo = J -m1x'1 * R + m2x'2 * R = (J+m1R²+m2R²)
Mo = Mp1 +Mp2 = m1gR-m2gR

donc ' = (m1-m2)gR / J+m1R² +m2R² et x2'' = (m1-m2)gR² / J + m1R²+m2R²
donc  ' = x2''*R

5)Donner l'expression de x''2 lorsque m1=m2. Est logique ?

X''2 = 0 lorsque m1 = m2, c'est logique puisque si m1= m2 il n'y a pas de mouvement, donc pas de vitesse, ni d'accélération.

6) Dans le cas où l'inertie de la poulie est négligée, ce qui revient à J=0, vérifier que l'accélération de l'objet (M2, m2) est beaucoup plus petite que g, à condition que m2 soit légérement supérieure à m1.

J=0 <=> x2'' = (m1-m2)gR² /  (m1+m2)R² = (m1-m2)g/(m1+m2)  négatif si m2>m1 donc on a bien x2'' beaucoup plus petite que g.


7)Dans le cas où les 2 masses sont différentes, exprimer les tensions T1 et T2 exercées sur chaque masse. Calculer leur différence et montrer que si l'on néglige l'inertie de la poulie, les tensions sont égales en norme.

relation fondamentale de la dynamique sur  l'axe Ox :

-ma =  T1 +P1 = T1 + m1g
ma = T2+P2 = T2 + m2g

T1 = -ma-m1g
T2= ma -m2g

T2 - T1 = -2*ma -m2g + m1g
… ne fonctionne pas.

autre méthode :

somme des moments des forces = J * accélération angulaire

donc  R(T1-T2) = J *
donc si J =0 :

R(T1-T2) = 0 donc T1= T2

Est-ce correctement justifié ?


Merci par avance pour toute aide apportée,