Inscription / Connexion Nouveau Sujet
Looping
Bonjour ! alors voila y'a quelque question qui me perturbe
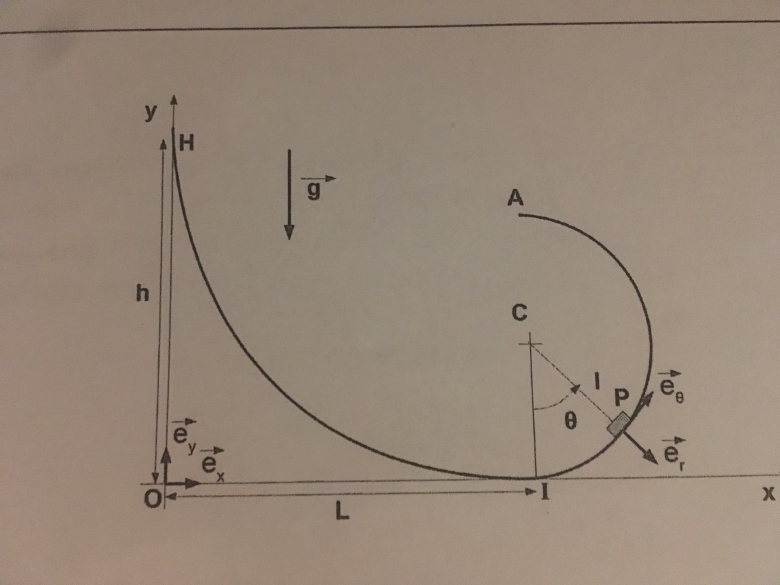
Le chariot qui se déplace sur le looping est assimilé à un point matériel P, de masse m. Celui-ci se déplace sur un rail situé dans un plan vertical. Le rail comporte une partie
constitué d'un demi cercle de centre C et de diamètre =2
On négligle tout frottement et la liaison entre le mobile et le rail est unilatérale, c'est-à-dire que le mobile se situe à l'intérieur de la rampe.La position du point P lorsque sa trajectoire est à l'intérieur du demi cercle est repéré par l'angle 
On désigne par g la norme de l'accélération de la pesanteur. A l'instant t=0, le mobile est libéré en H sans vitesse initiale à la hauteur H
j'aimerais particulièrement avoir de l'aide pour la question 4 et 7 si possible merci !
1)Montrer que le systeme est conservatif
J'ai dis que puisqu'on négligle les frottements et que la réaction normale des rails est perpendiculaire à la trajectoire alors le systeme n'est soumis qu'a son poid et c'est donc la seule force qui travaille, or le poid est une force conservatif
2)Exprimer en fonction de ,h,g et
La norme Vp de la vitesse du point P lorsqu'il est à l'intérieur du demi-cercle
Par une étude énergétique, variation d'enegie cinétique au point A et P je trouve que Vp=
(2g(h-cos(
))
3) Exprimer en fonction de
et la norme Vp de la vitesse du point P lorsqu'il est à l'intérieur du cercle
En utilisant les coordonnées polaires on trouve Vp=
4) On écrit la réaction de la rampe. Donner l'expression de R(
) au point P en fonction de
Je vais honnete, soit la question est mal formulée soit je suis aveugle, je pourrais le faire avec la 2ieme loi de Newton puis ensuite projetté R selon ey mais après j'ai la masse, l'accélération de la pesanteur dans l'équation .. enfin en gros juste avec je n'y arrive pas
5) A quelle condition sur le signe de R() la voiture reste-t-elle en contact avec le rail ?
Il doit etre strictement positive
6) Déduire des questions précédentes la hauteur minimale hm depuis laquelle on doit lacher le mobile sans vitesse initiale en H pour qu'il arrive jusqu'en A, point le plus haut du demi-cercle
Avec le PFD, puis injections des premières équation, et en prenant R(=
) je trouve que hm=
7) Donner dans ces conditions (h=hm), l'expression de la réaction R en
, point le plus bas
Je ne vois pas pour celle-la ..
Bonsoir
1) Le chariot est aussi soumis à la réaction des rails mais cette force ne travaille pas donc ta conclusion est correcte.
2)En P, l'altitude yp est égale à l.[1-cos()] ; ce n'est pas ce que tu as écrit me semble-t-il.
3) OK
4) il faut appliquer la relation fondamentale de la dynamique au chariot et la projeter suivant le vecteur er. Sachant que l'accélération normale centripète a pour norme , tu vas obtenir le résultat.
Je te laisse rectifier quand nécessaire. Tu pourras remarquer que le point I correspond au cas particulier =0.
Ah oui pardon petite faute de ma part pour la 2)
Mais du coup pour la 4) je vais pouvoir avoir l'expression rien qu'avec ? en faisant cela j'obtiens pas ce que je voulais :
Selon er j'ai :
m*a=m*g*cos()-R
Si je remplace l'accelération par j'aurai quand meme la masse, l'accélération de la pesanteur, enfin j'aurai pas uniquement
C'est vrai que la notation est un peu piégeante. R dépend de mais R ne dépend pas seulement de . Il dépend des autres paramètres dont tu parles dans ton dernier message.
Ok du coup je pense que j'ai toute les clées, l'accélération normale est de signe négative ?
si c'est comme tel ça va me donner que a=, ensuite je procède à une reinjection dans l'équation puis on isole R et j'aurai bien quelque chose en fonction de théta,
R=m+mgcos(
)
après on peut remplacer par l'expression trouvé en question 2)
Après simplification et compagnie je retombe sur la meme expression qui m'a permis de répondre à la question 6 :
R()=mg()
Annuler
connectez vous