Inscription / Connexion Nouveau Sujet
Longueur d'un ressort désenroulé
Bonjour,
mon sujet est "similaire" au post : ![]() longueur d un ressort
longueur d un ressort
Mais j'ai cru comprend que je devais en recréer un.
Je dois calculer la longueur détoronnée d'un câble, ce qui s'apparente à la longeur d'un ressort désenroulé (à vide).
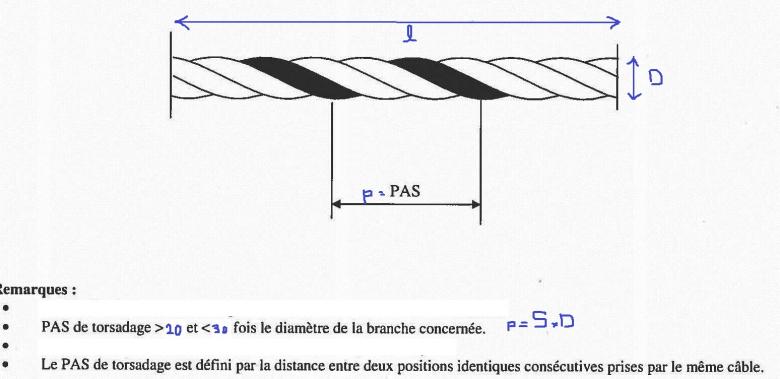
l= longueur de mon ressort.
D= diamètre de mon ressort
p(pas)=SxD avec S une constante.
Voici mon calcul, merci de m'indiquer mon erreur....
La formule pour calculer la longueur désenroulée d'un ressort étant:
L=n (Pi².D²+p²)
(Pi².D²+p²)
avec n le nombre de spire.
n=l/p
L=(l/p) (Pi².D²+p²)
(Pi².D²+p²)
L=(l/(S.D)) (Pi².D²+S².D²)
(Pi².D²+S².D²)
L=(l/(S.D)) (D²(Pi²+S²))
(D²(Pi²+S²))
L=(l/S) (Pi²+S²)
(Pi²+S²)
Et c'est là que ça me dérange, car mon diamètre n'intervient plus dans mon calcul.
Ce qui voudrait dire que ma longueur reste inchangée quelque soit le diamètre de mon toron. Et ça je sais que ce n'est pas le cas....
Développée d'une spire :
L1² = p² + Pi².D²
L1 = RCarrée(p² + Pi².D²)
nombre de spire : n = l/p
Longueur du câble : L = l/p * RCarrée(p² + Pi².D²)
---------
On pourrait s'arrêter là, mais ....
Si on a un ressort où p = S * D (S constante)
On peut évidemment remplacer p par S*D dans la formule donnat L.
L = l/(S*D) * RCarrée(S².D² + Pi².D²)
L = l/S * RCarrée(S²+ Pi²)
Donc ta réponse est correcte.
--------
On remarquera que ce soit dans L = l/p * RCarrée(p² + Pi².D²) ou bien dans L = l/S * RCarrée(S²+ Pi²), nulle part n'apparaît le diamètre du toron.
D n'est pas le diamètre du toron mais bien le diamètre de la spire du câble (qui est ici le diamètre extérieur de la spire - le diamètre du toron)
et avec en pratique D > > que le diamètre du toron.
Le diamètre du toron influence quand même car le pas est forcément >= diamètre du toron (et encore, le = n'est pas en pratique possible à cause du foisonnement).
Et donc, on ne peut pas choisir n'importe quoi comme pas, il doit tenir compte du diamètre du torons.
Sauf distraction. 
Merci pour la réponse et le temps passé.
Mais j'avoue ne pas être plus avancée 
Ici on prend D = diamètre du toron car en réalité la différence est négligeable.
Le diamètre du toron influence quand même car le pas est forcément >= diamètre du toron (et encore, le = n'est pas en pratique possible à cause du foisonnement).
Et donc, on ne peut pas choisir n'importe quoi comme pas, il doit tenir compte du diamètre du torons.
Sauf que dans ma formule finale, je n'ai ni le diamètre qui intervient, ni le pas.
Uniquement ma longueur et ma constante S.
Pour illusrer un peu mieux ma problématique:
Si je veux réaliser un faisceau de 10m avec un toron de 50mm, ce n'est pas la même chose que de réaliser un faisceau de 10m avec un toron de 10mm. Mais pas spécification de pas est la "même" (S*Diamètre de toron).
Comme c'était présenté au début ... on avait affaire à un câble de diamètre d enroulé sur un mandrin de diamètre D (avec forcément D > > d)
Certes le problème est proche, mais il est clair qu'ici, on ne peut pas faire l'approximation de D > > d
Néanmoins, si on veut réaliser 2 longueurs identiques de câble avec des "fils" de diamètres différents, on peut parfaitement conserver la même valeur de S
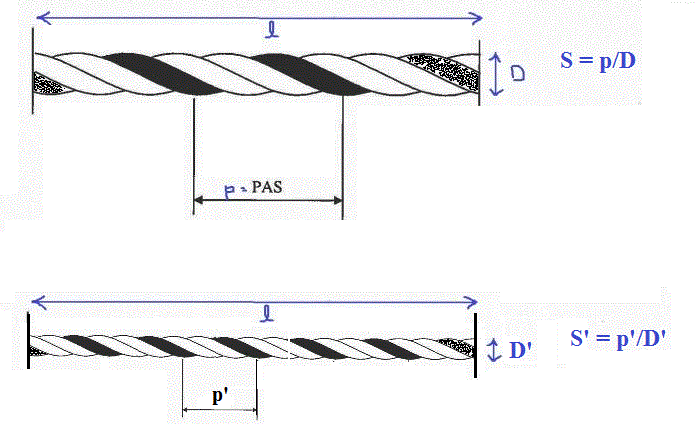
Dans mon dessin, S = S' (car D/D' = p/p')
Le dessin du bas est le même que celui du haut mais à l'échelle 1/2 ... sur un pas, une spire noire est 2 fois plus petite en bas qu'en haut ... mais il faut 2 fois plus de spires en bas qu'en haut pour réaliser une même longueur de câble.
Et donc, la longueur du fil noir est la même en haut qu'en bas.
Non ?

Dans mon dessin, S = S' (car D/D' = p/p')
Le dessin du bas est le même que celui du haut mais à l'échelle 1/2 ... sur un pas, une spire noire est 2 fois plus petite en bas qu'en haut ... mais il faut 2 fois plus de spires en bas qu'en haut pour réaliser une même longueur de câble.
Et donc, la longueur du fil noir est la même en haut qu'en bas.
Je pense que vous avez raison.
Mais les idées reçus ont la vie dure! je vais tester ma formule sur plusieurs câbles

Merci pour vos réponses.