Inscription / Connexion Nouveau Sujet
lois de coulomb
Bonjour
un explorateur de masse M, enroule son fouet sur une branche cylindrique (coeff de frott f=0.3) , l'explorateur peut il passer une rivière enpendulant sachant que le nombre d'enroulement est n=4.5?
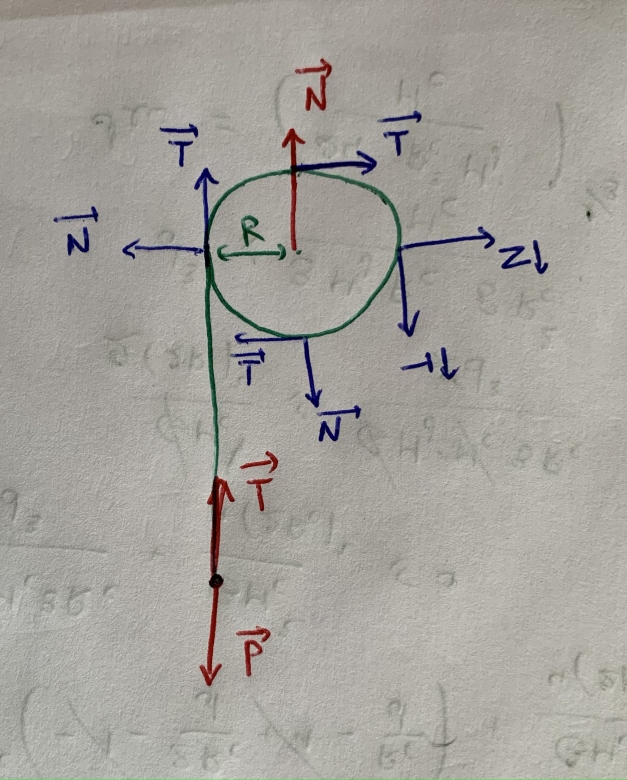
voici ce que j'ai essaye de faire jusqu'a present (schema en piece jointe)
1) laquelle des deux representations des forces sur mon schema (bleu ou rouge ) est elle correcte? sont elles les deux fausses?
2)manque t il des donnees dans l'enonce ? rayon de la branche? valeur numerique de M?
3)dans le cours on a plutot etudie des contacts plan /plan , or ici la zone de contact est circulaire/cylindrique j'ai donc pense a calculer la composante tangentielle elementaire en me placant a la limite de glissement
puis l'integrer ce qui a priori me semble logique car de sens oppose au poids
4) faut il utiliser les moments ? j'ai l'impression que oui mais je ne vois pas trop comment ?
merci a vous
Bonjour
J'ai déjà eu l'occasion d'aider sur un sujet analogue ici :
Mécanique 17
Sinon : pour ta représentation des forces, tout dépend du système choisi ; selon ce choix, les forces extérieures à prendre en compte ne sont pas les mêmes. Pour une force donnée, il faut toujours préciser par quoi (ou par qui) elle est exercée et sur quoi (ou sur qui) elle est exercée.
Bonsoir
apres consultation du lien que vous m'avez propose , j'ai quelque questions.
1) a quoi correspondent exactement les forces exerces par la droite et gauche du fil ( est qu'il s'agit de Fa et Fb ? ) du coup on considere que la tension du fil a gauche de M est homogene(constante le long du fil) et a droite de M aussi homogene mais de valeur differente Fb
2) en nommant Fd et Fg ( droite et gauche )
j'obtiens l'equation suivante ce qui est un peu different de l'equadiff que je suis sense trouver
3) aurriez vous une idee de pourquoi ma premiere approche est fausse, je ne vous cache pas qu'en voyant que mon intuition d'utiliser les forces élémentaires était la bonne voie, j'étais plutôt content, mais je n'arrive pas a comprendre ou se situe l'erreur dans la suite ?
4) qu'en pensez vous de ma question sur les moments ? j'avoue ne toujours pas avoir trouver de reponse.
merci a vous
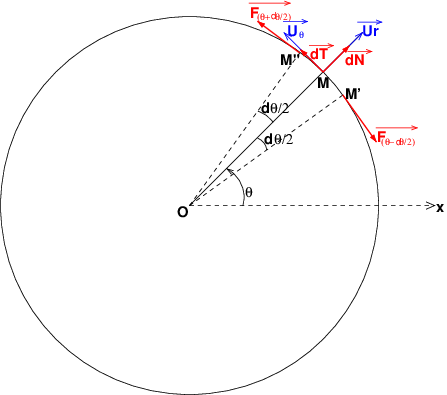
Ce schéma devrait t'aider. Le système dont on étudie l'équilibre par rapport à la branche (référentiel supposé galiléen) est la portion élémentaire de corde comprise entre M' et M" , centrée en M. Les deux forces notées F désignent les forces de tension exercées respectivement par la portion de corde situé à droite de M' et par la portion de corde située à gauche de M" (sur le schéma).
Pour un minimum de clarté, la figure n'est pas du tout à l'échelle.
d
est un angle élémentaire, supposé infiniment plus petit que l'angle . De même, les forces dT et dN sont des forces élémentaires supposées infiniment moins intenses que les forces F...
Tu peux maintenant reprendre l'aide apportée sur l'autre document...
Bonjour
j'avais fait un schema pareil pour les projections, toutefois c'est votre remarque sur les ordres de grandeurs de dT, dN et F qui me permet de dire que par PFS , F_g = F_d puis retrouver l'equadiff souhaite, toutefois je ne trouve pas ceci tres intuitifs , j'aurais natutellement plutot dit que dT et par consequent dN etait tres grande etant donne que c'est le 'frottement' qui permet de soutenir le poids de l'explorateur.Pouvez vous m'eclaircir ce point ?
merci
Relis bien les premières phrases de mon message du 09-08-16 à 17:13. Si B représente l'extrémité libre du fouet, FB=0 alors que, dans le cadre de l'approximation quasi statique : FA=M.g.
La tension F() n'est donc pas indépendante de comme tu sembles le penser mais décroît de façon monotone de la valeur Mg en =0 à la valeur zéro en =
.
Avec mes notations : F(+d/2)< F(-d/2).Cependant : le câble ne glisse pas sur la branche à cause de la force de frottement dT qui représente donc la différence entre les deux valeurs de tension précédentes.
Annuler
connectez vous