Inscription / Connexion Nouveau Sujet
Mécanique 17
Bonjour,
Voici un énoncé qui me donne du fil à retordre (vous allez comprendre le jeu de mots..et je suis désolé pour ça)
Indiana Jones () doit franchir une crevasse. Il enroule son fouet autour d'une branche. La branche a un rayon
et une corde de masse négligeable passe autour de celle-ci. Le coefficient de frottements est
. Quelle est la tension du dernier élément de fouet
en contact avec la branche si le fouet est enroulé 4,5 tours ?
Indiana franchira-t-il l'obstacle ?
En indication est donnée le texte suivant :
Pour résoudre ce problème il faut considérer que le fouet est un fil de masse négligeable, sans raideur, enroulé d'un angle sur un arbre cylindrique de rayon
, de génératrice l'axe des
. Le contact arbre-fil est
caractérisé par un coefficient de frottement . Indiana Jones
exerce une force sur l'extrémité
du
fil, il faut chercher la valeur minimale de la norme de la
force à appliquer à l'autre extrémité du fil pour qu'il soit
en équilibre.
Je ne vois pas du tout comment partir. Auriez-vous des pistes à me confier ?
Bonjour
Si je comprends bien l'énoncé, on peut supposer le fil en équilibre à la limite de glissement avec une tension du fil en A : et calculer la valeur de
qui annule puisque l'extrémité du fouet est libre. Si le calcul conduit à
9
, on pourra conclure qu'un enroulement de 4,5tours sur la branche est suffisant pour soutenir l'aventurier (approximation quasi statique).
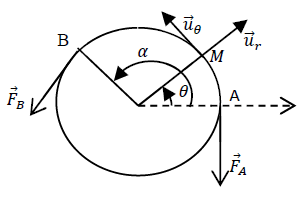
Méthode possible : isoler une portion élémentaire de fil centrée en M comprise entre (
-d/2) et (+d/2).
Faire l'inventaire des actions extérieures exercées sur cette portion :
La réaction normale de la branche :
La réaction tangentielle de la branche (force de frottement) : puisque nous sommes à la limite du glissement ; comme d'habitude, on considère que le coefficient de frottement statique est égal au coefficient de frottement dynamique.
La force exercée par la partie gauche (sur la figure) du fil :
La force exercée par la partie droite du fil :
C'est à ce niveau que les choses se compliquent : ces deux forces étant tangentes à la branche en (+d/2) et en (-d/2), ne sont pas colinéaires. Il faut s'intéresser aux projetés sur les deux axes de leur somme. On peut poser évidemment : .
Ensuite, la relation fondamentale de la statique projetée sur les deux axes doit te conduire à une équation différentielle (très simple d'ailleurs) te permettant d'obtenir l'expression de la tension du fil en fonction de .
C'est ce que j'avais commencé à faire, mais je n'avais pas centré M comme vous l'avez fais.
Je trouve, en approximant, l'équation différentielle , ce vous semble-t-il correct ?
Cela donnerait
Ton équa. diff. est correcte. Dans le cas général :
=.
Mais on ne peut pas annuler
Effectivement. Pour résoudre le problème, il faut supposer que l'extrémité du fouet possède une petite masselotte de masse m. L'enroulement du fouet étant de la forme (n+½ )tours avec n : nombre entier, tu peux écrire : FB=m.g
Fais le calcul : tu vas constater que m est vraiment une valeur très faible ; en pratique : faire un ou deux nœud(s) à l'extrémité libre de la lanière constituant le fouet peut suffire.
Ce problème de l'exponentielle qui tend vers zéro sans jamais être strictement nulle est récurrent en physique ...
Annuler
connectez vous