Inscription / Connexion Nouveau Sujet
Loi de Coulomb de frottements solide sur un plan 3D
Bonjour, je suis en cycle préparatoire (intégré) et je bloque sur un exercice de physique de descente sur une spirale. Je ne trouve pas d'exercice exactement similaire malheureusement. Je serais reconnaissante de l'aide de quelqu'un.
La question principale : est ce que la loi de coulomb sur un plan 3D est différente ? Comment j'utilise fRn= Rt dans cet exercice ? Je vous donne l'énoncé complet pour plus de clarté. Je suis principalement intéressée par les questions 7,8,9 mais si quelqu'un a le temps de le faire en entier ce serait vraiment apprécié !
Voici la transcription complète de l'exercice.
II. Descente d'une bille sur une hélice
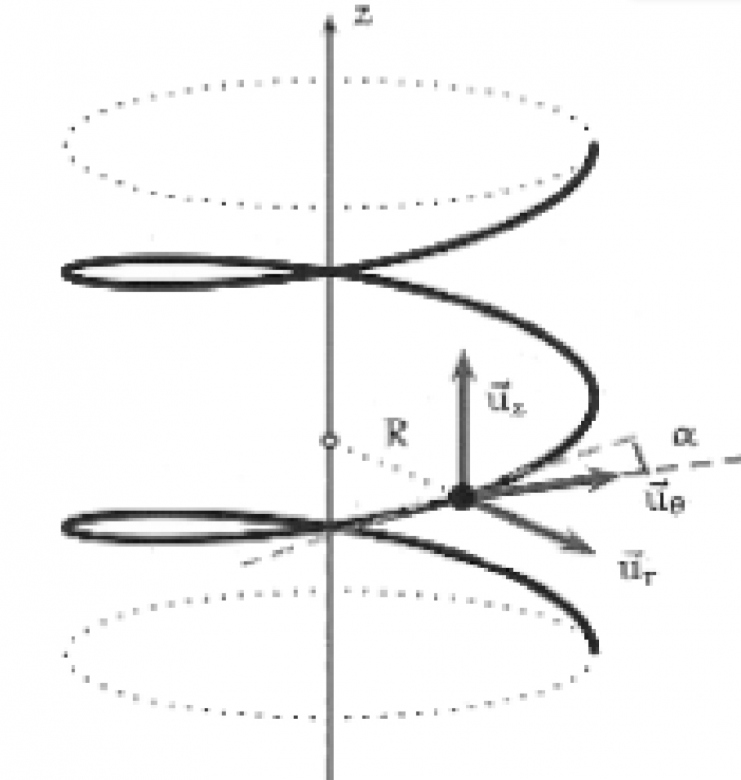
Un point matériel M de masse m se déplace sur une hélice d'équation
( r = R , θ = z / h ) en coordonnées cylindriques ( r , θ , z ), avec R > 0.
L'axe (Oz) est vertical ascendant (figure ci-contre).
On se place dans le référentiel R du laboratoire supposé galiléen.
Le point M est abandonné sans vitesse initiale depuis le point M₀ tel que
z = 0, θ = 0, et soumis au champ de pesanteur g⃗ = −g u⃗_z.
---
1.
a)
Exprimer le vecteur vitesse dans la base cylindrique
( u⃗_r , u⃗_θ , u⃗_z ), uniquement en fonction de la coordonnée z(t).
En déduire l'expression du vecteur unitaire u⃗_t tangent à la trajectoire et orienté vers le haut, dans la base cylindrique.
Quel angle α l'hélice fait-elle avec le plan horizontal ?
---
b)
On définit le vecteur unitaire u⃗_n orthogonal à la trajectoire par
u⃗_n = u⃗_r ∧ u⃗_t (produit vectoriel).
Calculer u⃗_n dans la base cylindrique.
---
Dans la suite, on écrira la réaction de l'hélice sous la forme
R⃗ = N⃗ + T⃗, que l'on décomposera dans la base ( u⃗_r , u⃗_t , u⃗_n ).
---
2.
Calculer le vecteur accélération dans la base cylindrique.
On l'exprimera uniquement en fonction de la coordonnée z(t).
---
3.
Projeter le principe fondamental de la dynamique dans la base
( u⃗_r , u⃗_t , u⃗_n ).
---
Dans un premier temps, on considère que la bille glisse sans frottement le long de l'hélice.
4.
Établir l'équation du mouvement pour la coordonnée z(t).
La résoudre.
---
5.
En déduire les composantes de la réaction R⃗ dans la base
( u⃗_r , u⃗_t , u⃗_n ) en fonction du temps.
---
6.
Par une approche énergétique, retrouver l'équation du mouvement.
---
On considère maintenant l'effet d'une force de frottement solide, qui est supposée vérifier la loi de Coulomb avec un coefficient de frottement f.
7.
Établir l'équation du mouvement.
---
8.
Déterminer la condition sur f pour que la bille glisse.
---
9.
Montrer qu'il existe une vitesse limite de chute, et l'exprimer en fonction des données.
Merci d'avance.
Bonjour,
Vous utilisez fRn= Rt qui, avec les notations de l'exercice, s'écrit T=fN.
Remarques :
Pour que cela corresponde aux lois de Coulomb, il faudrait une piste plate dont l'inclinaison transversale s'établirait de telle sorte que la normale à la piste ait la "bonne" direction : le vecteur est défini à partir de la trajectoire et il faut qu'il coïncide avec la normale au support pour appliquer les lois de Coulomb.
Il ne faut pas tout prendre au pied de la lettre, c'est un exercice purement scolaire : par exemple, dans la "vraie" vie, la bille roule.
Merci beaucoup de votre réponse !
Oui je comprends parfaitement ce que vous voulez dire. C'est un exercice scolaire donc quelques détails ne seront pas forcément réels. Le problème c'est que quand j'applique la relation que vous avez mentionné pour répondre à la question 8, j'obtiens l'expression suivante :
d²z/dt² (dérivée seconde de z)= -g/2(1-f). Ce qui m'a d'abord paru logique car l'angle alpha est π/4 donc tan alpha est π/4 = Rt/Rn mais pour la dernière question il faut trouver la vitesse limite.. ce qui n'aurait aucun sens si l'expression de l'accélération est celle ci?
Une autre suggestion par des amis à moi était d'utiliser la relation de telle sorte : Rt = f√[(Rr)²+(Rn)²], selon eux la normale devrait être la résultante.
Qu'en pensez vous?
gts2
Merci beaucoup de votre réponse !
Oui je comprends parfaitement ce que vous voulez dire. C'est un exercice scolaire donc quelques détails ne seront pas forcément réels. Le problème c'est que quand j'applique la relation que vous avez mentionné pour répondre à la question 8, j'obtiens l'expression suivante :
d²z/dt² (dérivée seconde de z)= -g/2(1-f). Ce qui m'a d'abord paru logique car l'angle alpha est π/4 donc tan alpha est π/4 = Rt/Rn mais pour la dernière question il faut trouver la vitesse limite.. ce qui n'aurait aucun sens si l'expression de l'accélération est celle ci?
Une autre suggestion par des amis à moi était d'utiliser la relation de telle sorte : Rt = f√[(Rr)²+(Rn)²], selon eux la normale devrait être la résultante.
Qu'en pensez vous?
Pour la question 8, je trouve :
Et le problème n'est pas dans T=fN puisqu'en 8) il y a uniquement Nn (Nr=0), et donc donne la même expression que
Où voyez-vous que ? (Je trouve
)
Je suppose que vous voulez dire qu'à la limite
Si , alors R=h et on trouve bien votre accélération
Donc en premier, vérifier ce
Pour la question 9), Nr n'est plus nulle, donc l'expression de T change et donc l'accélération aussi.
La relation de vos amis est bien la traduction de T=fN : la norme de (Nn,Nr) est bien
gts2
Pour alpha, après avoir trouvé le vecteur unitaire tangeant, le produit scalaire de celui ci avec u teta est égal à cos alpha, qui nous donne que alpha est π/4
J'ai lu vos réponses et je crois que j'ai compris la méthode à suivre. Je vous remercie de votre temps!
Je trouve une vitesse , soit un vecteur tangent
, dont le produit scalaire avec
donne
qui ne donne pas π/4.
gts2
C'est ce que j'ai trouvé moi:
Puis on dérive sachant que R constant
Après il reste à trouver le vecteur tangeant en divisant le vecteur vitesse par sa norme puis de faire le produit scalaire.
gts2
Je viens de voir que j'ai fait une erreur dans l'énoncé ! Je m'excuse. Teta = z/R, et non pas z/h. C'est la source de la contradiction.
OK, dans ce cas, votre résultat pour 8) est juste.
Pour 9), il faudra, comme déjà dit, prendre en compte Nr.
gts2
Oui, je ne sais pas si vous avez vu mais j'ai envoyé une deuxième réponse juste après mon raisonnement en relisant le votre. C'est là que j'ai remarqué la faute en recopiant l'énoncé. La version correcte c'est teta = Z/R. Je m'excuse de cette erreur.


