Inscription / Connexion Nouveau Sujet
Linéarisation d'une équation en mécanique
Bonjour à tous,
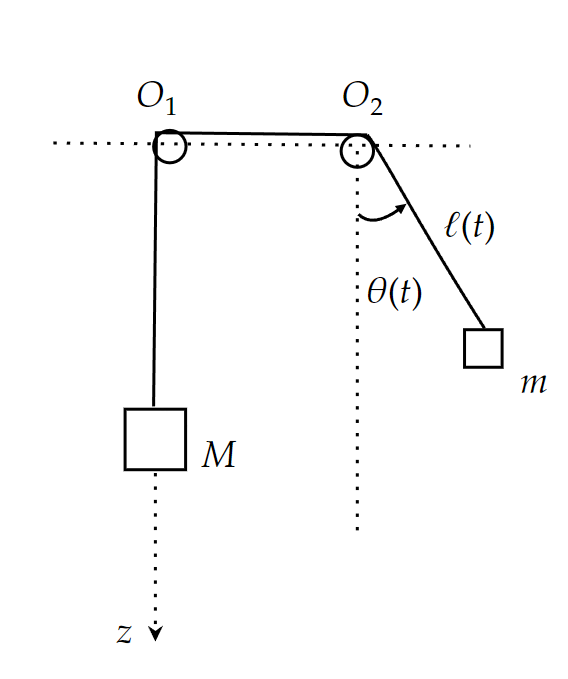
J'ai un problème concernant la linéarisation d'une équation en mécanique classique. On dispose de deux poulies auxquelles sont reliées deux masses M et m, la masse M pouvant uniquement se déplacer par translation selon un axe z descendant et la masse m étant reliée d'autre part à un système agissant comme un pendule simple d'angle .
Je vous épargne les calculs mais on arrive à l'équation
Je cherche à linéariser cette équation dans l'hypothèse de faible amplitude typiquement . Seulement voilà, quand je dois linéariser je sais que je dois obtenir seulement
.
Ma question est donc la suivante : où est passé le terme en ? Cela viendrait apparemment du fait que l'on pousse seulement le DL à l'ordre 1 et que ce terme est une ordre 2 mais je ne vois pas pourquoi ...
Le DL à l'ordre 1 autour de me donnerait
et donc par identification avec
on aurait
soit en multipliant par
:
ce qui ne colle pas avec le fait que ce soit négligeable.
Quelqu'un saurait comment m'aider?
Bonsoir
Difficile de t'aider sans plus de précision. Compte tenu de ce que tu as copié de l'énoncé,tu peux joindre l'intégralité de l'énoncé au format PDF. Un schéma précisant les notations et les conditions de fonctionnement est indispensable.
La linéarisation demandé correspond à un pendule simple de faible amplitude.
Merci pour le schéma. Sans énoncé complet, je risque de te dire des bêtises...Le théorème du moment cinétique conduit à l'équation différentielle que tu as écrite. L'étude de la masse M conduit sans doute à quelques chose de la forme :
Sous toutes réserves donc. Je pense tout de même qu'il faut se placer dans le cadre d'oscillation de faibles amplitudes, ce qui revient à un développement limité au voisinage de  =0. Dans ces conditions :
=0. Dans ces conditions : (développement au second ordre). Reste à montrer que dans les conditions de l'expérience (que j'ignore !!!) :
A la date , la masse m oscille et la masse M est lâchée sans vitesse initiale et le fil est inextensible.
C'est parfaitement ça (tu as fait les bonnes hypothèses pour les conditions initiales  ) mais pour arriver à avoir
) mais pour arriver à avoir je pense que t'as dû appliquer un théorème d'énergie pour ensuite linéariser l'équation obtenue (théorème de l'énergie mécanique par exemple).
Mon problème vient dans le fait de linéariser l'équation obtenue par un théorème du moment cinétique par exemple appliqué à m soit donc avec
ce qui donne
d'où mon premier message avec le développement limité.
Je n'ai pas de donnée supplémentaire sur l'angle, je sais juste que dans l'hypothèse de faibles oscillations, la linéarisation permet d'obtenir l'expression de que tu as mentionné. Je pense que tu t'es débarrassé de
car tu as considéré que c'était un ordre 2 mais j'aimerais comprendre pourquoi est-ce que ce terme est considéré comme ordre 2 puis pourquoi est-ce que cela permet de s'en débarrasser?
Il y a bien développement limité pour sin( ) mais pour le reste, il s'agit juste de voir si, dans le contexte expérimental, il est possible de négliger un terme devant l'autre en posant :
) mais pour le reste, il s'agit juste de voir si, dans le contexte expérimental, il est possible de négliger un terme devant l'autre en posant :
Sans plus de précision sur les données, cela me parait délicat.
Imagine par exemple M nettement supérieur à m : l'accélération de M est assez grande :
la valeur absolue de devient assez vite importante, la valeur de l diminue assez rapidement, la période propre d'oscillation du pendule diminue rapidement donc
augmente assez vite. L'inégalité
ne peut être satisfaite que pendant une durée très courte.
Si au contraire, l'écart entre M et m est assez faible, l'inégalité sera valide beaucoup plus longtemps mais la relation
deviendra fausse car il ne sera plus possible de négliger les variations de tension du fil dues aux oscillations du pendule.
Bref : tu ne fournis pas d'énoncé complet : cet énoncé existe-t-il ? Ne s'agit-il pas simplement d'un énoncé que tu as inventé en sous-estimant les difficultés d'une résolution rigoureuse ?
Le sujet était donné comme ça, il est apparemment issu d'un oral tombé l'an dernier mais je n'ai pas plus d'infos que ça, c'est juste que ça me paraissait bizarre de pouvoir négliger ce terme en faisant un DL à l'ordre 1.
Je me répète : négliger le terme en ne résulte pas d'un développement limité. Il s'agit juste, en réfléchissant aux ordres de grandeurs, de montrer qu'à chaque instant ce terme est négligeable devant l'autre terme de la somme. Ce qui revient à montrer qu'à chaque instant :
et cela est loin d'être évident sans plus de précision fournie par l'énoncé.
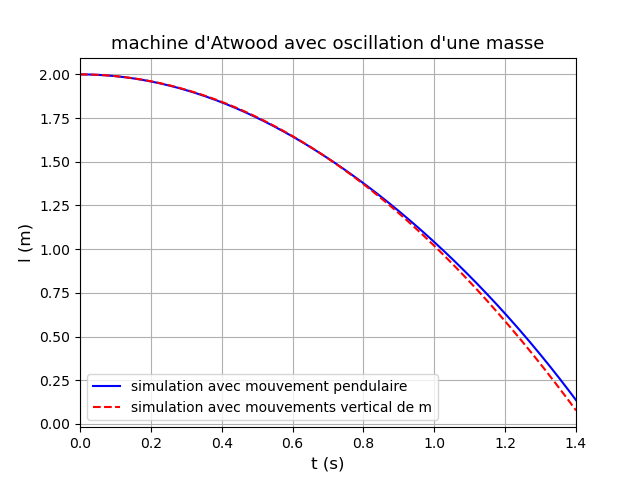
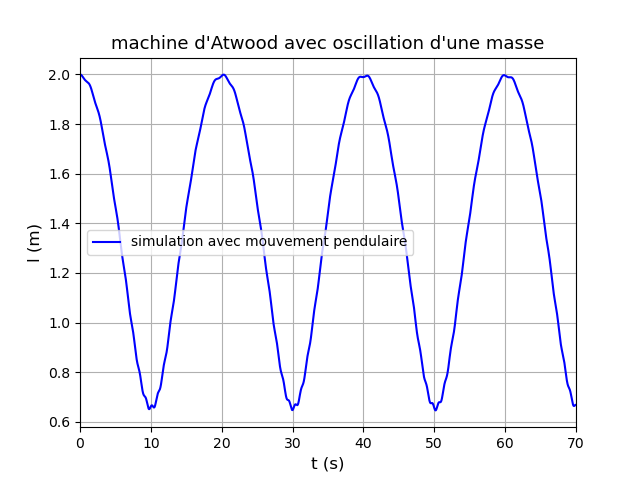
Pour illustrer mes précédents messages et la complexité du problème voici deux simulations théoriques effectuées sans approximations de calculs.On néglige cependant les frottement et l'inertie des poulies.
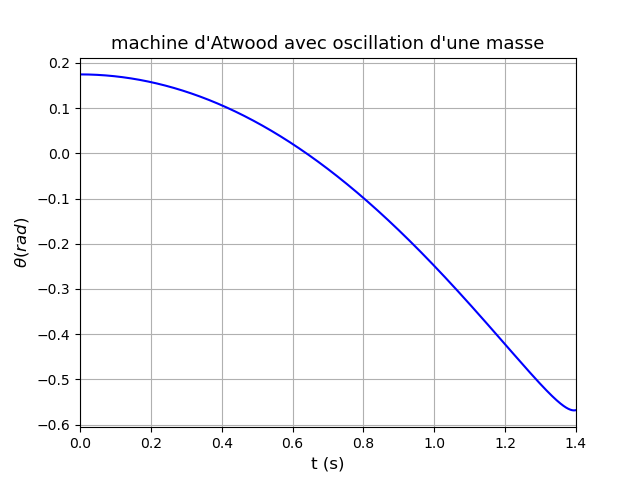
Premier cas : M=300g ; m=200g ; lo=200cm  o=10° :
o=10° :
Le mouvement d'oscillation de m influence très peu le mouvement de M mais impossible d'obtenir un mouvement d'oscillation avant que l ne devienne nul lorsque m atteint la poulie.
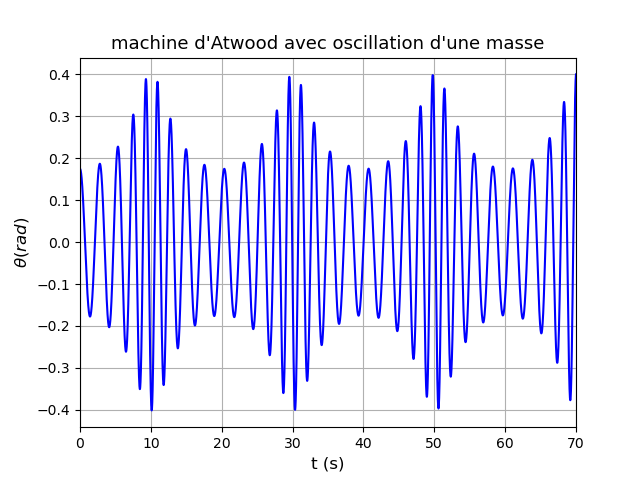
Deuxième cas : M=300g ; m=295g ; le reste inchangé.
on obtient un couplage entre deux mouvements d'oscillations : les oscillations pendulaire de m et un mouvement de va et vient en translation de M ; analogie avec deux oscillateurs couplés.