Inscription / Connexion Nouveau Sujet
Libre parcours moyen
Bonjour à tous 
J'ai une question à propos de la diffusion de particules de soluté en solution diluée, et plus précisément à propos de la démonstration de la relation r² =  ²/
²/
 t.
t.
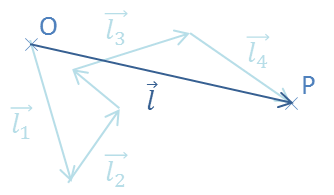
Dans cette démonstration, on s'intéresse à un grand nombre de particules, chacune subissant n chocs ( n déplacements li). La distance efficace parcourue par chaque particule est notée l (voir l'image ci-dessous pour n = 4).
n déplacements li). La distance efficace parcourue par chaque particule est notée l (voir l'image ci-dessous pour n = 4).
On exprime ensuite r² (carré de la distance moyenne de diffusion), qui vaut <l²> = n ².
².
Je vous épargne toute la démarche lol 
Mais pour pouvoir "intégrer"  dans la relation, mon prof a posé
dans la relation, mon prof a posé  ² = 1/n SOMME<li²>.
² = 1/n SOMME<li²>.
Pour moi,  est une moyenne classique (
est une moyenne classique ( 1/n SOMME<li>), mais si j'élève cette valeur au carré, je n'obtiens pas le terme précédent...
1/n SOMME<li>), mais si j'élève cette valeur au carré, je n'obtiens pas le terme précédent...
Je me suis renseigné et il me semble que mon prof a utilisé une moyenne quadratique (c'est bien çà ?), mais dans ce cas, n'est-elle pas supérieure à la moyenne classique ?
Dans ce cas,  ne serait pas vraiment le libre parcours moyen non ?
ne serait pas vraiment le libre parcours moyen non ?
D'ailleurs pendant qu'on y est, r = <l>, donc pourquoi r² = <l²> et non pas <l>² ? (il me semble que c'est le même problème...)
Merci d'avance, et désolé pour le roman ! 
Il y a plusieurs sortes de moyennes, parmi les plus connues, citons :
Moyenne arithmétique :
Moyenne géométrique :
Moyenne harmonique :
Moyenne quadratique :
Moyenne énergétique : le log étant en base 10.
L'utilisation des ces différentes moyennes dépend de l'application.
Sauf distraction.

Merci pour votre réponse 
Donc pour r :
- la moyenne arithmétique est <l>
- la moyenne quadratique est  <l²>
<l²>
Mais étant donné le contexte, je ne comprend pas pourquoi on utilise une moyenne arithmétique pour r (<l>) mais une moyenne quadratique pour r² (<l²>).
Normalement, r² = <l>²... alors pourquoi il est dit que r² = <l²> ?
Merci d'avance 
Qualitativement
Une voiture part en ligne droite du point A au point B (A et B sont distants de 100 km), en ensuite cette voiture fait un autre déplacement de B vers C de 100 km
Quelle est la distance entre les points A et C ?
Si vect(AB) = - vect(BC), alors |AC| = 0
Si vect(AB) = vect(BC), alors |AC| = 200
Il faut maintenant considérer tous les cas où les vect(AB) et vect(BC) ne sont pas colinéaires ... qui vont donner une distance intermédiaire entre 0 et 200.
On a 0 <= |AC| <= 200
Si on considère que l'angle entre les directions et sens de AB et BC ont une probabilité égale de se trouver n'importe où dans [-180° ; 180°], statistiquement la distance moyenne |AC| sera V2 * 100
Cela étendu à n déplacements successifs (n élevés), donnera que la distance moyenne entre le point de départ et le point d'arrivée (après n déplacements) est proche de la moyenne quadratique.
Tout ceci sans "rigueur", juste pour essayer de faire comprendre...
et sauf connerie de ma part.

Merci encore 
Que voulez-vous dire en disant "la distance moyenne |AC| sera V2 * 100" ?
J'ai tout compris jusqu'à cette phrase 
Bonjour,
Tu ne nous en dis tout de même pas beaucoup sur cette démonstration dans un domaine où les notations ne sont pas du tout normalisées. Pourrais-tu donner la signification exacte de tous les symboles que tu utilises ? Tu parles de diffusion de particules dans un milieu avec gradient de concentration : la démonstration qui te pose problème a-t-elle pour but de démontrer la loi de Fick ?
Sinon, il est exact que la valeur quadratique moyenne est supérieure à la valeur moyenne.
Bonjour 
Bah en fait j'avais peur que le message soit trop long et que personne n'ait le courage de lire 
En plus ce n'est pas tant la démonstration qui me pose problème mais certains outils statistiques^^
Non, ce n'est pas la démonstration de la loi de Fick et il n'y a aucun gradient de concentration : on considère juste une solution diluée et homogène, et on s'intéresse à la distance parcourue en moyenne par les particules de soluté (voir le schéma).
Au final, on obtient <l²> = n  ² =
² =  ²/
²/ t.
t.
Pour les notations :
- quand j'écris SOMME, c'est pour i allant de 1 à n
- et <...> signifie moyenne arithmétique de ... (on considère pleins de particules) : par exemple <li> c'est la moyenne du ième déplacement chez les particules
Il y'a deux choses que je ne comprend pas (mais en fait c'est un peu la même chose) :
- on s'intéresse à la distance moyenne r parcourue par les particules, mais si on calcule r² = <l²> c'est la moyenne des carrées des distances efficaces l : donc sa racine est la moyenne quadratique et non la moyenne
Donc dire que r est la distance moyenne c'est faux non ? A moins que moyenne arithmétique  moyenne quadratique ?
moyenne quadratique ?
- mon prof a posé que  ² = 1/n SOMME <li²> (j'ai mis du temps à comprendre cette relation, en gros on fait la moyenne des carrés des déplacements li pour chaque particule, et on fait la moyenne de ces moyennes
² = 1/n SOMME <li²> (j'ai mis du temps à comprendre cette relation, en gros on fait la moyenne des carrés des déplacements li pour chaque particule, et on fait la moyenne de ces moyennes  )
)
Donc  est la racine de tout ça et c'est aussi une moyenne quadratique...
est la racine de tout ça et c'est aussi une moyenne quadratique...
Voilà, dans les deux cas je ne comprend pas pourquoi r et  sont des distances moyennes, alors que dans les deux cas on les définis comme étant des moyennes quadratiques.
sont des distances moyennes, alors que dans les deux cas on les définis comme étant des moyennes quadratiques.
Je sais pas si je suis clair... désolé si ce n'est pas le cas je pourrais plus détailler 
Bonjour,
Si je comprends bien, il s'agit plutôt d'une étude type "mouvement Brownien".
Les quelques documents que j'ai pu consulter sur le sujet parlent tous de "déplacement quadratique moyen" et non de déplacement moyen. Ce qui semble te donner raison...
Merci pour votre réponse 
Oui c'est exactement ça ! Désolé si je n'ai pas été clair dès le début...
Donc la distance quadratique moyenne traduit l'importance du déplacement et permet de définir des grandeurs comme le coefficient de diffusion D, etc... mais n'est pas vraiment la distance moyenne parcourue. C'est bien ça ?^^
@ J-P : Finalement j'ai compris que V2 signifiait racine de 2  autant pour moi...
autant pour moi...
Vous dites que "la distance moyenne entre le point de départ et le point d'arrivée (après n déplacements) est proche de la moyenne quadratique" : comment êtes-vous arrivé à cette conclusion ? 


