Inscription / Connexion Nouveau Sujet
Les filtres
Bonsoir
Est ce que vous pouvez m aider sur un exercice que j ai pas compris comment proceder
Enoncé:
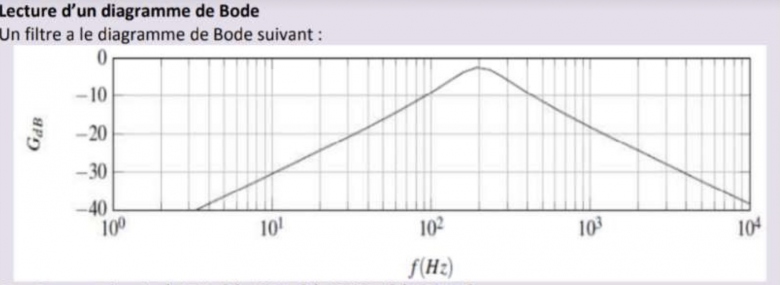
1-determiner le Gmax et pour quelle frequence f0 est il obtenue?
J ai trouvé Gmax= 10-0,15pour f=200Hz
2- determiner la largeur  f de la bande passante (en Hz) à 3dB?
f de la bande passante (en Hz) à 3dB?
J ai trouvé  f=210-190=20Hz
f=210-190=20Hz
3-Que valent les pentes des asymptotes ?
Je n y arrive je ne sais pas comment proceder
Mercu d avance
Bonsoir
Détermine graphiquement la variation du gain correspondant à une décade ( fréquence multipliée par 10 ).
Côté haute fréquence, la courbe se confond pratiquement avec l'asymptote aux fréquences supérieures à 103 Hz. Quelle estle coefficient directeur de cette portion de droite ? Tu sais ce qu'est une décade en fréquence ?
Étude analogue aux fréquences inférieures à 40Hz.
Une décade est l'intervalle de fréquence entre une fréquence f et la fréquence 10f.
Exemples :
Intervalle 102Hz - 103Hz
Intervalle 5Hz - 50Hz.
D accord
Mais ce que j arrive pas à comprende comment il faut proceder pour cette question les autres j avais des idees mais celle la je ne vois pas comment !
Je pense qu'ici, il faut raisonner sur les gains en décibels comme indiqué sur le diagramme de Bode. Que vaut Gmax exprimé en dB ?
Pour les pentes mesurées en décibels par décade : je t'ai indiqué les deux décades à étudier. Quelles sont les deux variations de gain correspondantes ?
Pour moi je croyais qu il fallait faire les tangantes pour les deux pendes et je regarde le point d intersection
??
Tu peux effectivement tracer les deux asymptotes obliques. Tu devrais vérifier que leur intersection a pour abscisse fo . L'énoncé demande de calculer les coefficients directeurs de ces deux asymptotes.
Les mathématiciens utilisent de préférence l'expression "coefficient directeur" plutôt que "pente" mais on peut considérer ces deux expressions comme synonymes ici. Je ne comprends donc pas ta phrase : "Mais le probleme avec le coef directeur je terouve pas pareil" ???
D'autant plus que les valeurs sont effectivement 20dB/dec à basses fréquences et -20dB/dec à hautes fréquences.
J'ai compris ce que tu veux dire !
Ton deuxième calcul aurait de l'intérêt seulement si l'axe des abscisses était gradué avec échelle linéaire mais, dans un diagramme de Bode, il s'agit d'une échelle logarithmique. De plus, avec une échelle linéaire, la courbe représentant les variations du gain en fonction de la fréquence n'admettrait pas d'asymptote oblique. Seul le calcul en décibels par décade (dB/dec) est pertinent.

 de -20
de -20
