Inscription / Connexion Nouveau Sujet
lentille plan convexe calculs
Bonjour, j'ai un exercice a résoudre qui consiste a demontrer que CF'=(nR)/ncosi-racine(1-n^2sin^2i) dans le cas d'un rayon qui arrive parallèle à l'axe optique avec une hauteur h par rapport à l'axe optique et qui passe par une lentille plan convexe de rayon de courbure R et d'indice n. on note P le point sur la lentille d'ou ressort le rayon, i l'angle entre le rayon incident et IC et I' l'angle entre le rayon qui ressort et IC. Je dois m'aider des sinus dans CIF', merci de votre aide..
Bonsoir
Commence par faire un schéma soigné que tu peux scanner et poster ici . Ensuite, la loi de Descartes sur la réfraction permet d'aboutir.
Ah oui pardon je vais le mettre ! J'arrive a trouver plein de relations mais pas a trouver celle demandée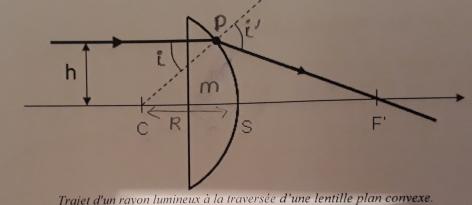
***Image recadrée => la partie texte doit être recopié***
La méthode est indiquée sous le schéma. Commence par exprimer en fonction de i et de i' les angles aux sommets du triangle (CPF) puis applique à ce triangle le théorème des sinus.
Annuler
connectez vous