Inscription / Connexion Nouveau Sujet
Lentille mince
Bonsoir, j'ai un peu de mal avec cet exercice, pourriez-vous m'aider s'il vous plaît?
On considère une lentille mince de centre O, d'indice de réfraction n1 et rayons de courbure S1C1 (à gauche) et S2C2 (à droite) en valeurs algébriques. La lentille est plongée dans un milieu d'indice n0.
1) Démontrer que la relation de conjugaison de la lentille est :
(1//OA) - (1//OA') = ( ( n1/n0) - 1)((1//OC2 - (1//OC1) )
2) et la distance focale f' est:
f' = -1 / [ ((n1/n0) - 1)(1//OC2 - (1//OC1) ]
3) En considérant n0 = 1, montrer que pour les lentilles :
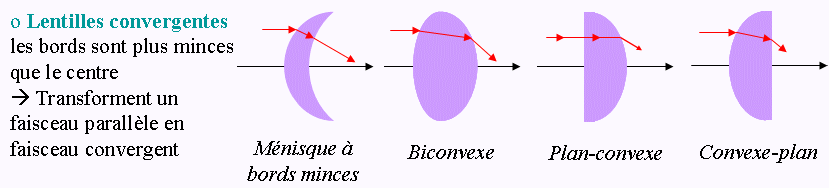
- biconvexe , ménisque convergente, plan-convexe: OF' > 0
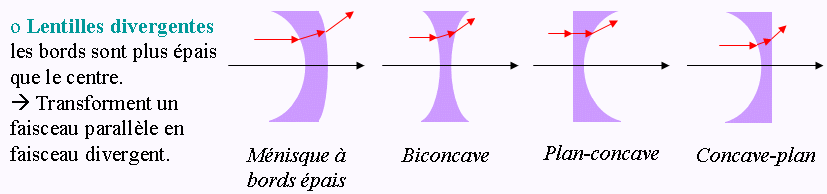
- biconcave, ménisque divergente, plan concave: OF' < 0
________________________________________________________________________________
1) Je penses qu'il faut considérer la lentille comme former par deux dioptres:
Pour le dioptre situé à gauche la formule est:
n0//S1A - n1// S1A'
Pour celui de droite:
n1//S2A - n1//S2A' = (n0 - n1)//(S2C2).
Comme il s'agît d'une lentille mince, je crois qu'on peut faire l'approximation qui donne S1 = O = S2 .
En replaçant S1 et S2 par O et en sommant les deux formules j'aboutis à:
1//OA - 1//OA' = [(n1 - n0)/(n1 + n0)]*(1//OC1) + [( n0 - n1)//(n1 + n0)]*(1//OC2)
Désolé pour l'écriture, mais je ne sais pas comment il faut faire pour obtenir de "vrai fraction". Je n'arrive pas à aboutir au résultat, je me suis peut-être trompé dans les relations dès le départ, je ne suis pas très sur de moi!
J'insère un schéma ci-dessous pour mieux comprendre.
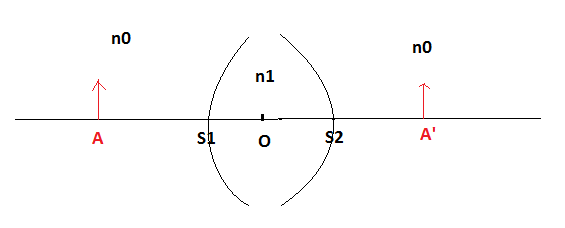
Bonjour mellissa,
merci d'avoir patiente. Je ne vois pas d'ou viennent les termes en 1/(n0 + n1) dans ton expression, mais peu importe. Ta methode est la bonne, et tu vas voir qu'elle conduit au resultat tres facilement.
La relation generale des dioptres spheriques avec origine en S s'ecrit n1/SA1 - n2/SA2 = (n1 - n2)/SC, ou A1 et l'objet, A2 son image, n1 et n2 les indices des milieux respectivement incident et emergent, et SC le rayon du dioptre. Les quantites en gras sont des grandeurs algebriques (mesures algebriques des segments correspondants).
On admet en effet que les sommet S1 et S2 des deux dioptres sont confondus en un point unique O. Donc pour le premier dioptre rencontre, en appelant A l'objet et A1 son image on ecrit n0/OA - n1/OA1 = (n0-n1)/OC1. Et pour le deuxieme, en appelant A' l'image du point A1 precedent, on ecrit n1/OA1 - n0/OA' = (n1-n0)/OC2. OK ?
Comme le terme n1/OA1 intervient dans chacune, on additionne membre a membre les deux equations et on obtient n0/OA - n0/OA' = -(n1-n0)/OC1 + (n1-n0)/OC2, ce qui en changeant les signes conduit bien a n0(-1/OA +1/OA') = (n1-n0)(1/OC1 - 1/OC2). En divisant par n0 on retrouve l'equation de ton enonce.
Distance focale image : on place A a l'infini pour avoir OA' = OF' = f', soit n0/f' = V, ou V = (n1-n0)(1/OC1 - 1/OC2) est la vergence de la lentille.
Distance focale objet : bien evidemment, on obtient n0/OF = -V.
Lentille biconvexe : OC1 > 0, OC2 < 0 d'ou f' > 0.
Menisque convergent : OC1 > 0, OC2 > 0 et OC2 > OC2 : f' > 0.
Plan-convexe : OC1 infini et OC2 < 0 : f' > 0.
Je te laisse continuer pour les trois autres cas. Tu peux t'aider d'un extrait de mon cours d'optique geometrique ci-dessous.
Si tu as des questions, n'hesite pas.
B.B.
Erratum : pour le menisque convergent, lire OC1 > OC2.
PS : connais-tu la relation de Gullstrand, qui permet de calculer la vergence V d'un systeme optique compose deux elements de vergences V1 et V2, non accoles comme les dioptres ci-dessus ?
Elle permet de montrer que si on ne suppose pas que les dioptres ont meme sommet en O, mais qu'on pose S1S2 = e, la vergence de l'association devient 1/f' = V = (n-1)(1/SC1 - 1/SC2) + e(n-1)2/(SC1.SC2), en posant n0 = 1 et n1 = n. Bien sur, si e = 0 on retrouve le resultat precedent.
Merci encore de m'avoir répondu pour la question 1 et 2, c'est tout bon.
Par contre j'ai un peu de mal pour la dernière.
En cours on avait vu que pour un dioptre convexe SC > 0 et pour un dioptre concave SC < 0. Mais par exemple pour la lentille " biconvexe" donc deux dioptres convexes mais pourtant on voit bien que S1C1 > 0 et S2C2 < 0. Ce n'est donc pas systématique?
connais-tu la relation de Gullstrand, qui permet de calculer la vergence V d'un systeme optique compose deux elements de vergences V1 et V2, non accoles comme les dioptres ci-dessus ?
Non je ne la connaissais pas, merci pour l'information!
soit n0/f' = V, ou V = (n1-n0)(1/OC1 - 1/OC2) est la vergence de la lentille.
Ce n'est pas plutôt 1/f' = V ?
pour le menisque convergent, lire OC1 > OC2.
Mais pourquoi ? car j'aurai plutôt dit le contraire car sur ma fiche d'exercice le dioptre 2 donc celui de droite est moins " courbé " que celui de droite donc pour le dioptre 2 le centre est plus éloigné et on aurait OC2 > OC1. Je ne comprends pas...
Et j'ai une dernière question: Si on change la position des lentilles , les dioptres s'inversent et le signe de S1C1 et S2C2 change donc également non? Ou alors ça n'a pas d'importance? Puisque sur ma fiche elles ne sont pas toutes orientées de la même façon que sur votre cours.
Oupss :
Pour le ménisque divergent
donc celui de droite est moins " courbé " que celui de droite
C'est plutôt : donc celui de gauche est moins " courbé " que celui de droite.


