Inscription / Connexion Nouveau Sujet
Le pouvoir des pointes
Bonsoir à tous.
J'ai essayé à plusieurs reprises un exercice sur le théorème mais je bloque, ainsi j'espère pouvoir être aidé.
Énoncé : Le pouvoir des pointes
Quel est le champ électrique rayonné par une sphère ( de rayon b1) conductrice chargé ( Q1) ? Quel est le potentiel autour de cette sphère ? Quel est le la sphère ?
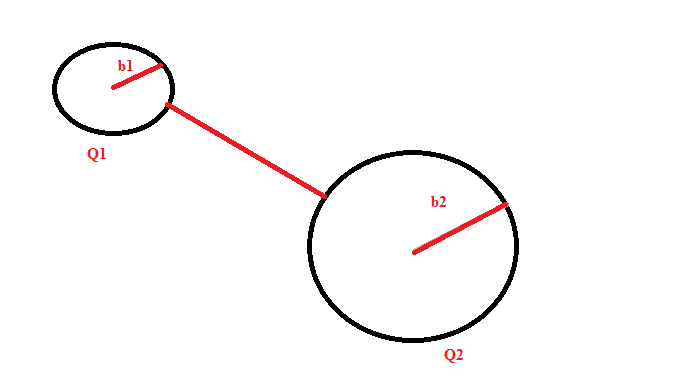
( Je vous joins le schéma )
On suppose maintenant que cette sphère est reliée à une autre sphère ( de rayon b2) par un long fil conducteur. Le fil est considéré suffisamment long pour que l'on puisse négliger l'influence d'un champ électrique sur l'autre.
Quelle sphère porte la charge la plus importante ? quel est le rapport entre les deux charges ? Pour faire le calcul, il faut écrire le potentiel de chaques sphère et souvenir qu'elles sont reliées pars un conducteur
Au voisinage de quelle sphère le champ électrique est-il le plus important ? Retrouvez vous le résultat connu ?
Bonjour,
Comme personne ne t'a porté secours ... je m'y colle (en plus il pleut!)
1) Champ électrique rayonné par la sphère 1
Je suppose que l'on s'interesse uniquement au champ en un Point M à l'extérieur de la sphére (on ne sait pas si elle est creuse ou pleine)
Soit don M un point dans l'espace tel que O1M⃗ = r.ur⃗ (O1 centre de la sphere 1)
E⃗(M) = Er⃗(M) + E
⃗(M) + E
⃗(M)
Pour des raisons de symétrie, on peut tout de suite dire que
E⃗(M) = 0⃗ et E⃗(M) = 0⃗
Le théroème de Gauss te dit ensuite très directement:
E⃗(M) = (1/4
0).Q.(OM⃗/r^3).ur⃗
2) Potentiel V autour de la sphère
E⃗ = -gradV⃗ s'écrit ici simplement Er = -dV/dr
Donc V(M) = -(Q1/40).(
dr/r2 entre r et +
avec V = 0 à + par convention
Donc V(M) = (Q1/40).(1/r)
3)
Quel est le la sphère ?
Je ne sais pas ... il manque des mots
4) On a maintenant relié les 2 sphères par un fil,
La conséquence est que la charge s'est répartie et que les 2 sphères se retrouvent au même potentiel
Soit q1 et q2 leurs charges resptectives
Tu peux exprimer V1 et V2 (potentiel à la surface des 2 sphères en fonction de q1 et q2),
Comme V1 = V2
Et que q1 + q2 = Q1 (la charge initiale de la boule 1)
Tu peux ensuite exprimer le champ électrique comme la somme (vectorielle) des champs des 2 sphères en appliquant les résultats de 1)
Au voisinage des sphères, tu peux simplifier la composition vectorielle, et je l'espère conclure...
Voili, voila,
Je ne connais pas le programme d'électromagnétisme dans ton cursus, donc n'hésite pas si certaines notions ne sont pas connues ou pas bien expliquée, je tenterai de reformuler ...
Annuler
connectez vous