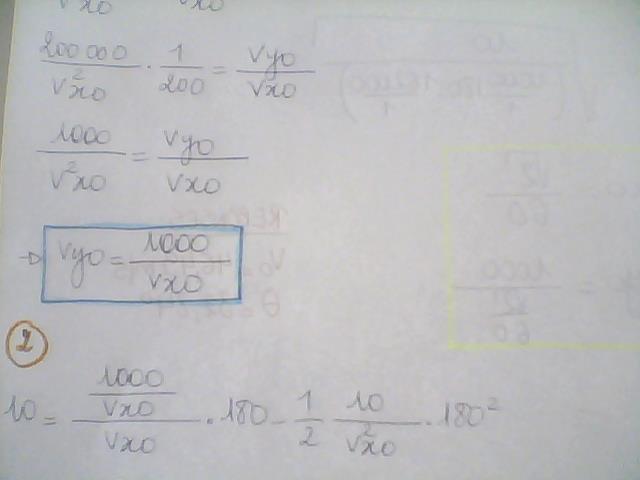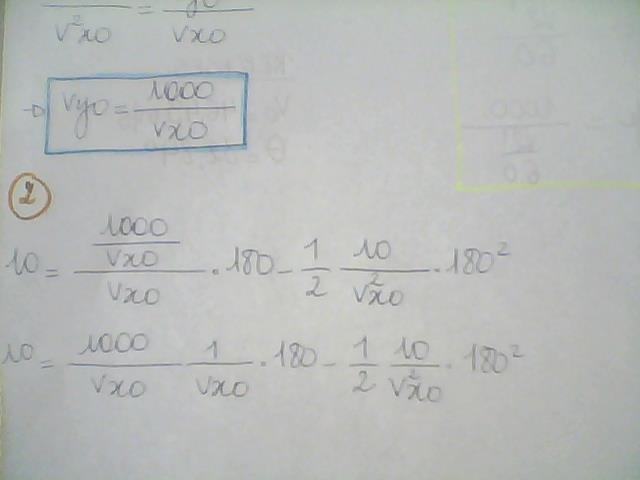Inscription / Connexion Nouveau Sujet
Lancer de balle de golf cinématique 2D
Bonjour,
je suis bloquée dans un exercice de cinématique 2D de mon cours de physique. J'aurais besoin d'un peu d'aide. Voici l'énoncé:
"La figure ci dessous schématise un parcours de golf. Le joueur désire envoyer la balle dans le trou situé en contrebas(drapeau). Le Green est toutefois bordé par un rideau d'arbres d'une hauteur de 12m. Déterminer la vitesse initiale(amplitude v0 et direction thêta) que le joueur doit communiquer à la balle si il désire que celle-ci frôle la cime des arbres et tombe directement dans le trou(sans rouler)."
J'ai appliqué les deux équations du mouvement selon x et y, en ayant pris la distance de 20 mètres pour x et la hauteur de 10 mètres(que je n'ai pas su placer dans mon calcul) pour y. J'ai rassemblé les deux composantes afin de trouver la vitesse initiale. Mais je n'obtiens pas la bonne réponse.
Cela est peut-être du à une erreur de calcul. Je remercie d'avance la personne qui prendra le temps de vérifier mon raisonnement et de me dire ce qui ne va pas.
J'ai malheureusement du poster mon schéma et mon raisonnement séparément, mon ordinateur ne me permettant pas de les rassembler en un bloc. J'éspère que cela ne rendra pas la compréhension de mon souci plus difficile. Merci.
Bonjour
Fournir un scan du schéma aurait effectivement été une très bonne idée. En revanche, il est demandé sur ce forum d'écrire sa solution plutôt que de scanner son brouillon.
Cependant, puisque je l'ai sous les yeux : c'est une très mauvaise idée de mélanger, dans une même formule, valeurs numériques et lettres. Il vaut mieux faire tout le raisonnement littéralement et terminer par l'application numérique. Cela donne plus de généralité à la solution et permet de détecter facilement les erreurs dues au manque d'homogénéité des formules...
Bonjour, merci de votre réponse. Je m'arrangerais à l'avenir pour me fournir un scan adapté. J'appliquerais également votre conseil de commencer à résoudre les équations littéralement et de poser les numéros par la suite. Mais pour cela j'ai besoin de savoir si mes équations de départ sont correctes. S'il vous plaît.
N'ayant pas la figure, mes notations risquent d'être erronées... Les équations horaires du mouvement sont, avec les notations les plus classiques, en posant x = y = 0 si t = 0 :
En éliminant t entre les deux, on obtient l'équation de la trajectoire :
La portée , c'est à dire ici la distance entre la position de départ et le trou, est la valeur non nulle de x qui annule y:
Tu connais sûrement la formule de trigonométrie :
Connaissant la valeur numérique de la portée, tu obtiens une première équation entre les inconnues et
.
Tu obtiens une seconde équation en écrivant que le point correspondant à la cime des arbres ( x = 10m , y = 12m si j'ai bien compris) appartient à la trajectoire. Cela te donne une seconde équation entre les inconnues et
. Ayant deux équations pour deux inconnues, tu dois pouvoir t'en sortir...
Merci beaucoup. Vraiment. J'ai vraiment du mal avec cet exercice. Excusez-moi, le site refusait de publier mon schéma tout à l'heure. Le voici.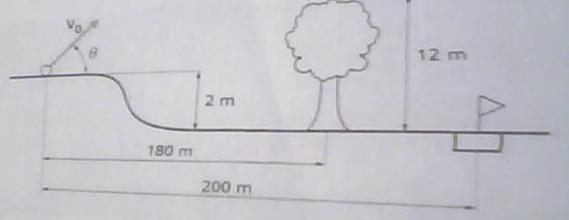
** image recadrée **
C'est un peu moins simple que je ne le pensais : le trou et la position de départ ne sont pas dans le même plan horizontal. La notion de portée ne va pas t'être utile ici. Il faut simplement partir de l'équation de la trajectoire et écrire que les deux points suivants appartiennent à cette trajectoire :
le trou : x1=200m ; y1=-2m ;
la cime de l'arbre : x2=180m ; y2=10m.
Cela te donne encore deux équations pour deux inconnues.
D'accord, y1 vaut donc -2 mètres. Je pensais qu'il valait 0. Je vous remercie d'avoir pris le temps de me répondre, je vais essayer de cette manière. Au revoir
Bonjour,
Comme Vanoise te l'a rappelé (que je salue), il faut recopier les énoncés et les propositions de solution sur le forum avec les outils mis à disposition.
Merci de le faire la prochaine fois.
Pour cette fois-ci je laisse ta proposition en l'état.
Bonjour, j'ai pris en compte vos remarques. Malheureusement je n'ai pas trouvé de scan ou de logiciel pour scanner mes documents. Auriez-vous quelque chose à me suggérer? Quant au site même, je n'ai pas trouvé le paramètre me permettant de le faire.
Mes excuses. Je vous remercie.
Bonjour
Je ne comprends ton message précédent : le scan que tu as posté de ton schéma est parfaitement clair !
Salut,
Tu n'as pas compris mon propos, je parlais de ton message du 08-08-16 à 12:42 --> il faut taper cela à la main avec les outils à disposition pour les formules.

Bonjour, en réponse à vanoise: il ne s'agit pas d'un scan malheureusement. Mais d'une photo que j'ai prise depuis mon portable. Je ne possède pas de scan.
gbm: Je taperais tout à la main la prochaine fois. Je m'excuse encore. Merci.
Bonjour
Faute de mieux, continue à poster les schémas comme tu l'as fait avec ton portable et écris l'énoncé et ta proposition de solution.
x(t) = Vo.cos(theta) * t
y(t) = 2 + Vo.sin(theta) * t - gt²/2
frôle des arbres :
x(t1) = Vo.cos(theta) * t1 = 180
y(t1) = 2 + Vo.sin(theta) * t1 - gt1²/2 = 12
Tombe dans le trou :
x(t2) = Vo.cos(theta) * t2 = 200
y(t2) = 2 + Vo.sin(theta) * t2 - gt2²/2 = 0
On a donc un système de 4 équations à 4 inconnues (t1, t2, Vo et Theta) :
Vo.cos(theta) * t1 = 180
2 + Vo.sin(theta) * t1 - g.t1²/2 = 12
Vo.cos(theta) * t2 = 200
2 + Vo.sin(theta) * t2 - g.t2²/2 = 0
On élimine t1 et t2 :
2 + Vo.sin(theta) * 180/(Vo.cos(theta)) - g.[180/(Vo.cos(theta))]²/2 = 12
2 + Vo.sin(theta) * 200/(Vo.cos(theta) - g.[200/(Vo.cos(theta)]²/2 = 0
Avec g = 10 m/s² :
2 + 180.tg(theta) - 10.[180/(Vo.cos(theta))]²/2 = 12
180² = (36.tg(theta) - 2).Vo².cos²(theta) (1)< ---
2 + 200.tg(theta) - 10.[200/(Vo.cos(theta))]²/2 = 0
5*200² = (2 + 200.tg(theta)).Vo².cos²(theta)) (2)< ---
(2)/(1) -->
5 * (200/180)² = (2 + 200.tg(theta))/(36.tg(theta) - 2)
theta = 0,57324 rad (32,844°)
et remis dans (1) --> Vo = 46,49 m/s
Calculs non vérifiés. 
mmalou edit (pour ce qui écrit en rouge)
Bonsoir, ***, j'ai réussi à faire l'exercice grâce à l'aide de vanoise. Je viens de voir le message de J-P. Je n'ai pas le même développement (j'ai quelque chose de tout de même plus simplifié) mais sur la fin nous nous rejoignons, j'ai également des tangentes à la fin et exactement la même chose. Par contre je ne savais pas qu'il fallait poster automatiquement sa réponse lorsqu'on avait résolu un exercice. Je le ferais à l'avenir.
Merci à tous pour votre aide.
Bonjour
Par contre je ne savais pas qu'il fallait poster automatiquement sa réponse lorsqu'on avait résolu un exercice.
Pas nécessairement poster la réponse mais juste signaler que tu avais réussi : cela fait toujours plaisir de savoir que l'aide apportée à été efficace !
Si tu as besoin d'aide à nouveau : surtout n'hésite pas !
Bonjour,
Je suis sur le même exercice , je ne comprends pas une seule ligne dans le développement de J-P ( 2)/(1) -->
5 * (200/180)² = (2 + 200.tg(theta))/(36.tg(theta) - 2)
Je ne comprends pas ce calcul. Merci de m'éclairer!
Bonjour
Des lignes et des lignes de calculs sans justifications et sans utilisation de l'éditeur d'équations comme dans ce message du 19-08-16 à 13:52 : cela ne facilite pas la compréhension en effet...
La plupart des formules utiles ont été justifiées ici : message du 08-08-16 à 18:14.
Y a-t-il quelque chose que tu ne comprends pas dans la théorie ?
Bonjour Luc21Y
je ne suis pas responsable de ce qui a été écrit plus haut 
mais, je suis allée te flécher ce que l'auteur avait appelé (2) et (1)
Bonjour vanoise, messages croisés
Voilà, tu reprends la main pour explications si nécessaires...j'en suis bien incapable
Je suis tout a fait d'accord . Je suis allé tres doucement et j'ai compris ne vous inquiétez pas Vanoise .
J'ai bien identifié ce que l'auteur nomme (2)/(1) . Mais mon problème est que lorsque je fais le calcul , je n'aboutit pas a ce qu'il trouve lorsqu'il fît le rapport !
On part de l'équation démontrée dans mon message du 08-08-16 à 18:14 :
que l'on écrit sous la forme :
La trajectoire doit passer par le point de coordonnées : x1=200m ; y1=-2m et par le point de coordonnées : x2=180m ; y2=10m . Cela conduit à un système de deux équations à deux inconnues :
Division membre à membre :
On obtient :
Ensuite :
Avec g=9,81m/s2 (inutile d'arrondir à 10 avec les moyens de calculs modernes), on obtient :
vo=46,0m/s