Inscription / Connexion Nouveau Sujet
La transformée de Fourier et son interprétation
Bonjour,
j'aurais besoin d'informations quant à ce que l'on a coutume d'appeler " l'analyse spectrale d'un signal " (un son dans mon cas). Comment la définir formellement ?
D'après mes recherches, il semblerait que ce qu'on appelle le spectre d'un signal soit le module de la transformée de Fourier de ce signal. Est-ce bien ça ?
J'ai effectué le calcul du module de la transformée de Fourier d'un petit enregistrement personnel (le mot "bonjour" enregistré par le micro de mon ordinateur, dont j'ai tronqué les silences avant de le normaliser avec le logiciel audacity), et voici le résultat avec le logiciel Matlab : 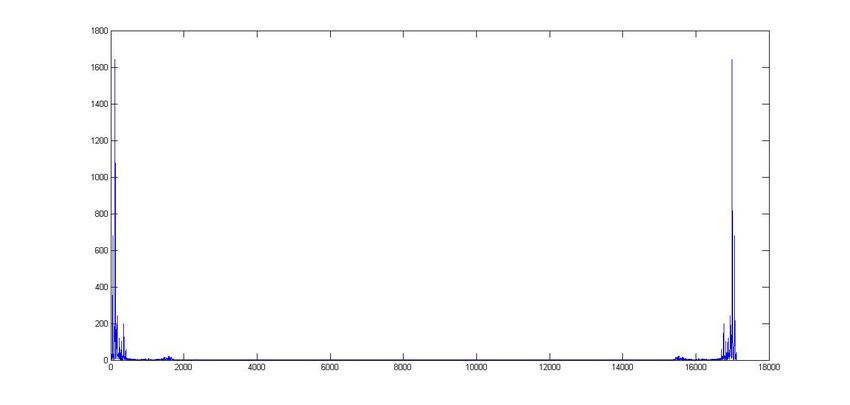
Ce graphe semble symétrique, qu'est-ce qui justifie cela ? Il ne ressemble pas à ce que l'on a coutume d'appeler un spectre il me semble. En effet la fonction pwelch de Matlab appliquée à mon signal (pxx = pwelch(x) returns the power spectral density (PSD) estimate, pxx, of the input signal, x using Welch's overlapped segment averaging estimator) rend un graphe qui semble bien différent : 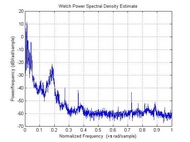 (les restrictions sur la taille du fichier ne m'autorisent pas à mettre une image plus grande que ça...)
(les restrictions sur la taille du fichier ne m'autorisent pas à mettre une image plus grande que ça...)
J'ai une hypothèse qui serait que la deuxième image ne soit qu'une partie de la première (comme si seules les premières fréquences avait été conservées). Est-ce le cas ? Si oui, pourquoi le spectre de pwelch (qui est visiblement le même que celui d'audacity :  ) ne conserve-t-elle qu'une partie du module de la transformée de Fourier du signal ? Comment est déterminée la dernière fréquence conservée ?
) ne conserve-t-elle qu'une partie du module de la transformée de Fourier du signal ? Comment est déterminée la dernière fréquence conservée ?
Merci ! 
Edit Coll : forum modifié
Bonjour,
N'y connaissant rien, je vais essayer de t'aider 
Comme indiqué il y a peu sur une autre post la TF d'un signal représente la densité (plutôt appelée contribution) fréquentielle du signal. La TF transforme en effet une fonction du temps: qui représente le "niveau" d'un signal dans le temps en une fonction
qui est le niveau de ce signal par Hertz.
ça c'était ta première question
Pour la deuxième ça se complique, je ne connais pas audacity et je ne sais comment tu a "injecté" ton signal sonore dans matlab. Mais réflexions donc plutôt que mes éclaircissements:
Si le signal en entrée de la fonction est le "bonjour" il semble "louche" de trouver des fréquences dans le zone 17 kHz (on est là dans les harmoniques de certains instruments la voie humaine plafonnant à <10 kHz avec des sons comme "ssssssss")
Par contre, il serait intéressant d'obtenir des informations sur l'estimateur utilisé par audacity pour fournir le périodigramme.
EtuOu de renouveler, si possible, l'expérience avec un son "monotone" grave
Bonjour,
Je m'y connais peut-être un petit plus...
Le spectre du signal est effectivement le module de la transformée de Fourier du signal.
Mathématiquement,une transformée de Fourier est une intégrale qui donne les fréquences contenues dans un signal dépendant du temps (on peut appliquer la transformée de Fourier sur d'autres signaux). La transformée de Fourier calculée par un logiciel est précédée d'un échantillonnage temporel et l'intégrale est transformée en somme discrète (transformée de Fourier rapide ==> FFT).
Sur la première figure, la fréquence d'échantillonnage est 9 kHz. La partie du spectre située à droite est en fait la partie négative du spectre. Plus exactement, c'est la partie "négative" du spectre d'ordre 1.
Un signal réel a un spectre qui présente une symétrie hermitienne. Le module est pair (symétrique par rapport à 0). Donc on représente le plus souvent la partie positive, surtout que les fréquences négatives ne "passent" pas bien en général...
Je peux donner des détails mathématiques mais le niveau "autre" n'est pas très explicite...



