Inscription / Connexion Nouveau Sujet
la trajectoire d'une particule
Bonsoir
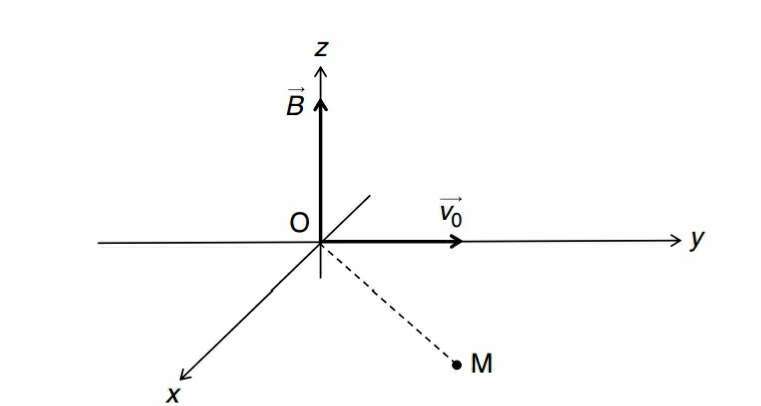
Une particule ponctuelle chargé positivement avec une charge Q, de masse m , est introduite à l'instant t=0 avec une vitesse initiale 
dans une région de l'espace où règne un champ magnétique uniforme vectB.
Dans l'ensemble de l'exercice , on négligera le poids de la particule compte tenu de l'intensité des autres forces mises en jeu .
Montrer que la trajectoire de la particule est un cercle contenu dans le plan (Oxy) et passant par O . Déterminer le rayon de cette trajectoire en fonction du champ magnétique , de la masse de la particule, de sa vitesse initiale et de sa charge .
Q = 10^-6 C , Vo= 20 m/s , B=10^-1 T , m= 3×10^-9 kg .
franchement cette situation est un petit peu différente pour moi , je demande vos propositions ou bien de voies pour commencer et merci
Bonjour,
Vous avez un problème de mécanique du point et usuellement vous le traitez ainsi :
- on définit de quoi on parle : système, référentiel ...
- on fait le bilan des forces
- on applique un principe ou un théorème
Ici il n'y a pas de raison de changer. Qu'est-ce que cela donne dans ce cas ?
OK.
Donc la force magnétique n'est pas nulle.
Puisque vous connaissez Frenet, projetez cette relation dans la base de Frenet.
l'accélération tangentielle + l'accélération normale
puisque on a la vitesse constante donc l'accélération tangentielle est nulle
donc l'accélération ici vaut v²/R
cela montre que la trajectoire est un cercle ?
pour le rayon comment on va le déterminer ?
je pense que le vecteur du champ magnétique est perpendiculaire au vecteur vitesse donc le produit vectoriel entre eux vaut Vo×B
donc la force magnétique F=qVoB
on va obtenir qVoB=m×V²/R
c'est vrai ?
Si l'accélération tangentielle est nulle que dire de v ?
Et donc comment se simplifie votre équation ?
Il suffit d'ajouter la projection sur Oz de F=ma, pour montrer que et qu'on a donc une trajectoire plane dans le plan Oxy.
Tout est constant dans R= m×V/Q×B, donc R=Cte, la trajectoire est plane, donc ...
Oui c'est ça
mais je sais pas pourquoi j'ai pas remarqué tous ça dès le début ...avez-vous des conseils concernant cela ?
Si c'est la première fois que vous voyez qqch du genre, il n'est pas anormal de ne pas voir du premier coup.
Sinon, une remarque d'ordre général : ne pas hésiter à s'appuyer sur le texte pour aider l'intuition : on ne vous demande pas de trouver la trajectoire, mais de montrer que c'est un cercle, donc on sait où l'on va.
Annuler
connectez vous