Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

la poussée totale effective

Posté par
nano21 12-08-17 à 12:58

bonjour tout le monde,
Pourriez- me corriger cet exercice svp?
merci d'avance.

voici l'énoncé:

Un réservoir cylindrique, à fonds circulaires plats, repose horizontalement sur une génératrice et est rempli d'un liquide de poids volumique ϖ jusqu'à la hauteur de son axe. Les dimensions du cylindre sont les suivantes : longueur l  , rayon r.
Exprimer la poussée totale effective sur chaque fond et sur la surface demi-cylindrique, et déterminer les centres de pression sur les trois parois.

Application- l  = 4m ;  r=2m ;   le liquide est de l'eau ;    g=9.81 m/s²




Exprimer la poussée totale effective sur chaque fond et sur la surface demi-cylindrique

Rappel :
La poussée effective en un point du liquide est la pression due au liquide seulement, en ne tenant pas compte de la pression atmosphérique


Avec :
F = la force pressante en Newton
ρ =  la masse volumique de l'eau   = 1000 [kg/m³]
h =  la hauteur (ou hauteur d'eau) en [m]
L'accélération de la pesanteur = g = 9,81 (N/kg)
ϖ=poids volumique du liquide en (N/ m³ )=  ρ * g

F = ½  ρgLπR²
F= ½ (1000  x  9.81  x 4 x π2²)
F=246552  N




La poussée totale sur la surface demi-cylindrique est de :

F  = ρgLπ(r/2)²
F=  ϖ  x 1 x π ( r/2)²  

F  = 9810x1 x 3.14 ( 2/2)²  

F  = 30803,40 N




Déterminer les centres de pression sur les trois parois :

Le centre de pression (points d'application de P1 et P2 ) est sur l'axe HI à une profondeur HC donné par la formule :

HC = (Mi/Ms)  

Avec
Mi =moment d' inertie du 1/2 cercle par rapport à son diamètre=1/2 moment d' inertie du cercle=(πr^4)/8  

Ms =le moment statique  

Mi/Ms=   ( (πr^4)/8)/((π4r^ )/(2 x 3x π))=(  3π)/3


Les centres de pression sur les trois parois =   (  3π)/3

Posté par
vanoisere : la poussée totale effective 12-08-17 à 18:29

Bonjour
Cela ressemble beaucoup à l'exercice précédent mais en plus compliqué.
Pour la paroi demi-cylindrique. L'étude de l'équilibre de l'eau puis l'application du principe des actions réciproques permet d'affirmer que la force de poussée exercée par l'eau est de vecteur opposé au vecteur poids de l'eau ; en norme :
F1=.g.Veau
Je crois que ce que tu as fait est correct.
Pour les parois verticales (demi disques) : quel est ton raisonnement ? Tu ne trouves pas bizarre que L intervienne dans le résultat ? Modifier la valeur de L à r fixe tout en maintenant le récipient à demi rempli ne change pas la pression et ne change pas la surface pressée...

Posté par
vanoisere : la poussée totale effective 12-08-17 à 23:17

Citation :
Je crois que ce que tu as fait est correct.

Je crois que je me suis montré bien optimiste en lisant trop vite ce que tu as écrit ! Oublie cette phrase et ce qui suit dans mon premier message.
L'expression :
F=.g.Veau = ½  ρgLπR²
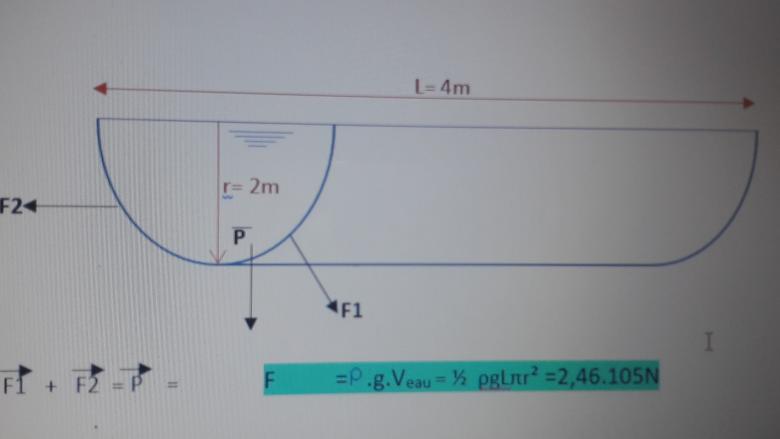
désigne, par étude de l'équilibre de l'eau et par application du principe des actions réciproques, la résultante des forces de pressions exercée par l'eau sur les trois parois, ce que tu peux appeler la poussée totale. Cependant, comme les actions sur les deux parois verticales (les fonds) sont horizontales et se compensent entre elles, la poussée totale est aussi égale à la force  exercée par l'eau sur la paroi demi cylindrique :
F=.g.Veau = ½  ρgLπR² =2,46.105N
La force de poussée exercée par l'eau sur un fond vertical nécessite un calcul intégral car la pression dépend de la profondeur z : il faut découper la parois en bandes élémentaires de largeur dz , où la pression effective de l'eau vaut :
P(z)=.g.z
Le calcul n'est pas totalement évident car la largeur de chaque bande élémentaire dépend de z. Il faut t'aider d'un schéma...
Je te laisse réfléchir et proposer une solution.
Pour les trois centres de poussées :
* sur la surface demi cylindrique : aucun calcul nécessaire ! Le raisonnement ressemble beaucoup à celui que je t'ai exposé concernant la surface sphérique. (L'as tu compris ?)
* sur chacun des fonds : un calcul intégral est nécessaire ; la position du centre de poussée sur chacune de ces parois dépend de r...
Attention : la physique ne se résume pas à l'application de formules plus ou moins compliquées !

Posté par
nano21re : la poussée totale effective 13-08-17 à 14:19

Bonjour vanoise (je viens de voir ta réponse ...je t'en remercie)

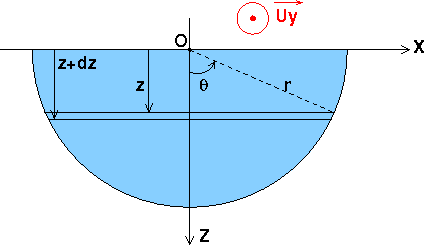
Donc ce que j'ai compris pour trouver les poussées de pression sur les bases verticales du cylindre, on représente une section droite circulaire, son centre O et le niveau d'eau qui affleure au niveau de O qui représente l'axe du cylindre

La force pressante dépend de la profondeur; donc on prend un élément de Surface horizontal ,repère par sa distance , verticale , z au centre O et d'épaisseur dz:

Cette élément de Surface = dS= dz*2(r^2-z^2)^1/2

Exprimant  l'élément de force pressante sur dS:

                 dP=wg.z*dS
                 dP=wgz.dz.2(r^2-z^2)^1/2

Posté par
nano21re : la poussée totale effective 13-08-17 à 14:25

...mon schéma initial

la poussée totale effective

Posté par
vanoisere : la poussée totale effective 13-08-17 à 18:01

Tu es sur la bonne voie en ce qui concerne la détermination de la force de poussée F2 sur une des deux parois verticale en forme de demi disque (un des deux fonds). Attention à ne pas confondre masse volumique et "poids volumique" : expression considérée comme obsolète. La force élémentaire de poussée sur une bande élémentaire déjà définie s'écrit :

\overrightarrow{dF_{2}}=P_{(z)}.dS.\overrightarrow{U_{y}}

\overrightarrow{U_{y}} étant un vecteur unitaire perpendiculaire à la paroi orienté vers l'extérieur du récipient. Cela conduit à :
\\ dF_{2}=P_{(z)}.2\sqrt{r^{2}-z^{2}}.dz=2\rho.g.z.\sqrt{r^{2}-z^{2}}.dz

F_{2}=2\rho.g.\int_{0}^{r}z.\sqrt{r^{2}-z^{2}}.dz

On peut trouver au moins trois méthodes différentes permettant d'obtenir l'expression de F2. Je te les exposes rapidement ; à toi de choisir ensuite celle qui te parait la plus adaptée à ton niveau.

1° On peut remarquer que le calcul intégral est analogue à celui qui permettrait d'obtenir la cote du centre de gravité d'une plaque homogène ayant la forme d'un demi disque. La méthode, analogue à celle de Guldin, permet d'obtenir directement le résultat sans calcul mais cette méthode n'est peut-être pas à ton programme :

\int_{0}^{r}2z.\sqrt{r^{2}-z^{2}}.dz=\frac{\text{volume de la boule de rayon r}}{2\pi}=\frac{2}{3}r^{3}

Donc :

F_{2}=\frac{2}{3}\cdot\rho\cdot g\cdot r^{3}

2° Calcul direct de l'intégrale en posant : u=r^{2}-z^{2}\quad et\;donc\quad du=-2z.dz

F_{2}=-\rho\cdot g\cdot\intop_{r^{2}}^{0}\sqrt{u}\cdot du=\frac{2}{3}\rho\cdot g\cdot\left[u^{\frac{3}{2}}\right]_{0}^{r^{2}}=\frac{2}{3}\cdot\rho\cdot g\cdot r^{3}

3° Calcul de l'intégrale à peine plus long que le précédent, ayant l'avantage d'être plus facilement transposable à la détermination de la position du centre de poussée demandée ensuite.

z=r.\cos\left(\theta\right)\quad;\quad dz=-r.\sin\left(\theta\right).d\theta\quad;\quad\sqrt{r^{2}-z^{2}}=r.\sin\left(\theta\right)

F_{2}=-2\rho.g\cdot r^{3}\cdot\int_{\frac{\pi}{2}}^{0}\cos\left(\theta\right)\cdot\sin^{2}\left(\theta\right)\cdot d\theta=2\rho.g\cdot\int_{0}^{\frac{\pi}{2}}\sin^{2}\left(\theta\right)\cdot d\left(\sin\left(\theta\right)\right)

F_{2}=2\rho.g\cdot r^{3}\cdot\left[\frac{sin^{3}\left(\theta\right)}{3}\right]_{0}^{\frac{\pi}{2}}=\frac{2}{3}\cdot\rho\cdot g\cdot r^{3}
Je te laisse réfléchir à l'étude des centres de poussée. N'hésite pas à poser des questions sur ce que je viens d'écrire si tu le juges utile.

la poussée totale effective

Posté par
nano21re : la poussée totale effective 13-08-17 à 22:09

Vanoise je ne peux pas te remercier assez pour ton aide précieuse

Posté par
vanoisere : la poussée totale effective 19-08-17 à 18:07

Bonjour nano21
Voyant que tu bloques toujours sur la notion de centre de poussée (centre de pression) voici quelques explications supplémentaires.
Je vais partir de l'analogie avec la force de pesanteur (poids) qui, comme les forces de pression, est une force répartie et non une force appliquée en un point précis. Le poids est une force à répartition volumique : chaque volume élémentaire constituant un solide possède un poids élémentaire et la résultante de ces poids élémentaires constitue le poids du solide. Le centre de gravité est le point particulier de l'espace où le moment du poids est nul quelle que soit l'orientation du solide dans l'espace. Au lycée, tu as certainement vérifié qu'une plaque métallique mince est en équilibre indifférent sur la pointe d'un compas si cette pointe verticale coïncide avec le centre de gravité de la plaque. On montre aussi (théorie des torseurs sans doute pas à ton programme) que le moment du poids dans le cas général se calcule comme si le poids était une force appliquée au centre de gravité du solide. Cela fait dire parfois (à tort bien sûr) que le centre de gravité est le point d'application du poids.

En statique des fluides, les forces de pression exercées par un liquide sur une paroi sont à répartition surfacique. Il existe un point particulier appelé centre de poussée qui a des propriétés analogues au centre de gravité :
1° : le moment en ce point des forces de pression est nul :
2° : dans le cas général : le moment des forces de pression se calcule comme si les forces de pression étaient une force égale à leur résultante appliquée au centre de poussée. Attention au « comme si » : le centre de poussée n'est pas le point d'application puisqu'il s'agit de forces à répartition surfacique.
La propriété n° 1 est très utile pour déterminer le centre de poussée à partir des éléments de symétries de la surface : cas de la calotte sphérique précédemment et ici : cas de la surface demi cylindrique. Par analogie avec le raisonnement que je t'ai fait pour la calotte sphérique précédemment, tu devrais être capable de démontrer que le centre de poussée est sur l'axe de symétrie du récipient cylindrique (axe (O,y) de mon schéma, à la distance L/2 d'un fond ; résultat d'ailleurs valide quel que soit le niveau de remplissage du récipient.
La propriété n°2 permet d'obtenir le centre de poussée sur l'un des fonds en forme de demi disque. Par raison de symétrie, ce point Cp est sur l'axe (O,z). Pour obtenir la position de ce point, je calcule le moment résultant de la force de poussée sur le fond par rapport à l'axe (O,x) de deux façons différentes (voir mon schéma du message précédent):
Première méthode : Le moment résultant par rapport à (O,x) de la force élémentaire s'écrit :

dM_{Ox}=dF_{2}.z=P_{(z)}.2\sqrt{r^{2}-z^{2}}.z.dz=2\rho.g.z^{2}.\sqrt{r^{2}-z^{2}}.dz

M_{Ox}=\rho.g.\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz
Deuxième méthode : Ce moment se calcule comme celui de la résultante F2 appliquée en Cp :

M_{Ox}=F_{2}.z_{Cp}
Donc :

z_{Cp}=\frac{\rho.g.\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz}{\rho.g.\int_{0}^{r}2.z.\sqrt{r^{2}-z^{2}}.dz}=\frac{\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz}{\int_{0}^{r}2.z.\sqrt{r^{2}-z^{2}}.dz}

L'intégrale au dénominateur a déjà été calculée. Si on ne perd pas de vue que 2.\sqrt{r^{2}-z^{2}} représente la largeur de la bande élémentaire, on remarque que celle au numérateur peut se calculer en remarquant qu'elle intervient dans le calcul du moment d'inertie par rapport à l'axe Ox (noté IOx) d'une plaque homogène de densité surfacique \sigma :

I_{Ox}=\sigma.\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz

Or, le moment d'inertie d'une telle plaque vaut :

I_{Ox}=\frac{1}{4}m.r^{2}=\frac{1}{4}\cdot\sigma\cdot\frac{\pi.r^{2}}{2}r^{2}=\frac{1}{8}\cdot\sigma\cdot\pi\cdot r^{4}

\frac{1}{8}\cdot\sigma\cdot\pi\cdot r^{4}=\sigma.\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz\quad donc\quad\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz=\frac{1}{8}\cdot\pi\cdot r^{4}

D'où la profondeur du centre de poussée sur un fond :

\boxed{z_{Cp}=\frac{\frac{1}{8}\cdot\pi\cdot r^{4}}{\frac{2}{3}\cdot r^{3}}=\frac{3\pi}{16}\cdot r}

Remarque 1 : certain livres pose \sigma=1 dans la mesure où cette valeur disparaît ensuite du calcul. Je ne conseille pas ; cela fait perdre le contrôle sur l'homogénéité des formules, ce contrôle étant un moyen de déceler de grosses étourderies de calcul. Et puis : écrire qu'un moment d'inertie puisse être égale au produit d'un volume par une distance...

Remarque 2 : à moins de disposer de tables sur les moments d'inertie ou d'être familier de ce type de problème, l'expression du moment d'inertie n'est pas évidente. On peut donc effectuer le calcul intégral en utilisant la méthode n°3 décrite dans le message précédent. Il suffit de remplacer z par son carré :

N=\int_{0}^{r}2.z^{2}.\sqrt{r^{2}-z^{2}}.dz=-2r^{4}\int_{\frac{\pi}{2}}^{0}\cos^{2}\left(\theta\right).\sin^{2}\left(\theta\right).d\theta=\frac{r^{4}}{2}\int_{0}^{\frac{\pi}{2}}\sin^{2}\left(2\theta\right).d\theta

N=\frac{r^{4}}{4}\int_{0}^{\frac{\pi}{2}}\left[1-\cos\left(4\theta\right)\right].d\theta=\frac{r^{4}}{4}\left[\theta-\frac{\sin\left(4\theta\right)}{4}\right]_{0}^{\frac{\pi}{2}}=\frac{1}{8}\cdot\pi\cdot r^{4}

Avec cela, j'espère que tu va être capable d'obtenir la position du centre de poussée sur la plaque en forme de trapèze de l'exercice suivant. Le calcul intégral est beaucoup plus facile !

Posté par
nano21re : la poussée totale effective 21-08-17 à 21:47

Bonsoir vanoise...Tout d'abord merci beaucoup de m'offrir de ton temps pour répondre à mes questions ...désolée je ne t'ai pas répondu (j 'ai été un peu malade )...

je ne suis pas revenue vers toi concernant le centre de poussée , par ce que j'ai appliqué directement une formule donnée dans le cours :


"pour un paroi demi-circulaire   : le centre de pression , point d'application de P1 et P2 est sur l'axe OZ à une profondeur OC donné par le formule:  
OZ=Mi/Ms      
Mi= r^4/8
Ms= r²/2     4r/3=2r^3/3

OZ=r^4/8   * 3/2r^3=   3r/16"

Posté par
vanoisere : la poussée totale effective 22-08-17 à 14:42

Tu as donc bien utilisé cette fois-ci ton formulaire. Effectivement, l'emploi d'un formulaire permet de gagner du temps, surtout lorsque le calcul est assez technique comme ici. Il ne dispense pas de réfléchir et c'est bien en réfléchissant aux propriétés du centre de poussée que l'on peut obtenir, sans le moindre calcul, la position du centre de poussée dans le cas d'une calotte sphérique (exercice précédent) ou dans le cas d'une surface demie cylindrique comme ici.
Et puis, il y a des cas  - par exemple : exercice suivant sur la plaque en forme de trapèze - où le calcul intégral est plus simple qu'un découpage compliqué de la surface afin d'utiliser le formulaire.
Bon courage !

Posté par
nano21re : la poussée totale effective 22-08-17 à 16:35

l'exercice suivant sur la plaque en forme de trapèze je ne l'ai pas  revue encore  (je viens de répondre le boulot aujourd'hui)....mais je dois le faire ce soir..je reviens vers toi Vanoise encore  (donc soit prêt )...je te remercie beaucoup Vanoise pour ton aide.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !