Inscription / Connexion Nouveau Sujet
la poussée total
bonjour,
pourriez -vous vérifier svp la première partie de ma réponse relative au problème suivant:
Un réservoir a la forme d'un tronc de cône dont les dimensions sont les suivantes : hauteur h, rayon de la base inférieur r , rayon de la base supérieure R. (R>r).
Le fond est constitué par une calotte sphérique dont la hauteur est égale au cinquième du rayon de la sphère.
Calculer la poussée totale sur le fond d'une part, et sur la paroi tronconique d'autre part, lorsque le réservoir est plein d'un liquide de poids volumique ϖ, déterminer également, la position du centre de pression sur le fond.
h= 3m ; r= 3m ; R=4m ; le liquide est de l'eau ; g=9.81 m/s².
Calculer la poussée totale sur le fond :
La poussée exercée par le liquide est proportionnelle à la masse volumique de ce liquide, à l'accélération de la pesanteur g et à la profondeur h à laquelle on prend la mesure.
Tout d'abord calculons le volume du réservoir.
Il y a deux parties :
Le volume de tronc de cône cylindrique
La calotte sphérique du bout.
1) le volume du cylindre vaut
= 116.24 m3
2) calotte sphérique
Le volume est donné par la formule :
Vcal= (πh² )/3 x (3 r-h)
Volume de la calotte sphérique en m3
calotte sphérique dont la hauteur est égale au cinquième du rayon de la sphère. :
r'=5 et h=1
V2 = 14.67 m3
Le volume total suivant les dimensions données vaut :
V1 + V2= 116.23 m3 + 14.67 m3
soit le volume total = 130.89 m3
Donc :
Avec
H : la hauteur de liquide( h1+h2)
S : étant la surface du fond de la calotte sphérique = 2π* r*h=18.85m²
ϖ= ρ g = 1000 x 9.81= 9810 N
La poussée totale exercée par le liquide sur le fond est de :
P = Patm + ρ⋅g⋅ H . S
P= 1000 x 9.81x18.85
P= 184914N
La poussée totale exercée par le liquide sur la paroi tronconique est :
Avec
h: la hauteur =3
S : étant la surface latéral de la calotte sphérique = S = π × ( R + r ) × a
ϖ= ρ g = 1000 x 9.81= 9810 N
p .g.h/2 . S
La résultante des forces qui s'exercent sur une paroi est égale au produit de la pression effective au centre de gravité de cette paroi par la surface de cette paroi.
La position du centre de pression sur le fond??
je vous remercie encore une fois
Bonjour
Je ne sais pas quel âge peut avoir cet énoncé mais la notion de "poids volumique" a disparu du vocabulaire scientifique depuis au moins cinquante ans.
Pour le reste :
P = Patm + ρ⋅g⋅ H . S
Revoie bien ton cours : cette formule est fausse !
Tu as raison de calculer le volume de liquide, cela va servir !
Ensuite, tu dois exprimer la pression en fonction de la profondeur z.
Le calcul de la force pressante exercée sur la paroi tronconique n'est pas simple : la surface n'est pas plane et la pression augmente avec z ! Il faut découper cette surface en bandes élémentaires de hauteur dz, calculer la force pressante élémentaire exercée sur cette bande puis intégrer sur toute la hauteur du tronc de cône. Attention : les composantes horizontales de ces forces pressantes se compensent par raison de symétrie alors que les composantes verticales s'ajoutent.
Pour la calotte sphérique, un calcul intégral analogue est possible. On peut cependant s'en passer en remarquant que la somme des forces pressantes sur la calotte sphérique et la paroi tronconique s'exprime simplement sans calcul puisque le volume de liquide est connu. Alors, par différence...
Bref : cet exercice est beaucoup plus difficile qu'il n'en a l'air...
Je te laisse réfléchir à ce que je viens d'écrire et proposer une solution...
Réflexion faite : on peut même se passer de tout calcul intégral pour calculer les deux forces pressantes mais il faut bien réfléchir...
bonsoir
d'abord je vous remercie pour votre réponse ..
j'ai commencé a répondre à la question correspondant à la poussée totale exercée par le liquide sur la paroi tronconique ...(mais je ne suis pas sure de moi ..pourriez vous me dire si je suis sur la bonne piste)
La poussée totale exercée par le liquide sur le fond est en fonction de la profondeur H :
P = ρ⋅g⋅ H
P= 1000 x 9.81 x 4
P= 39240 N
La poussée totale exercée par le liquide sur la paroi tronconique est :
La force hydrostatique qui s'appliquent la paroi tronconique (une surface courbée) peut être obtenue par le calcul des composantes horizontales et verticale.
F = √((F² H + F² V ).)
La composante verticale est égale a :
Verticalement : FV = W (le poids du volume de liquide compris entre la paroi et la surface libre)
W = ρ.g.Vp avec Vp : est le volume du corps de pression
W= 1000*9.81*116.24m3
Horizontalement :
avec
La surface élémentaire « dS » est situé à une profondeur de « h », la pression qui s' y exerce est : P =ϖh
Donc la force élémentaire sera : ∫ dF =ϖhdS ⇒ F = ϖhdS
dS est la projection horizontale de la surface courbée = dz x 2(r²-z²)1/2
.......
Merci
Tu es loin du compte ; tu sembles parfois confondre poids et pression. D'autre part, par raison de symétrie, la résultante horizontale des forces de pression sur la paroi tronconique est nulle.
Je t'explique en quelques mots la méthode sans calcul intégral. On imagine que la calotte sphérique est enlevée et remplacée par un disque horizontal de rayon r. Le nouveau récipient ne contient plus que 116,23m3 d'eau mais la pression exercée par cette eau est la même en tout point de la paroi tronconique qu'avant. La force de pression exercée par l'eau sur la paroi tronconique est donc la même. Plutôt que de faire un calcul intégral, on s'intéresse à l'équilibre de l'eau ; celle-ci est soumise aux forces suivantes :
son poids (valeur connue)
la force de pression exercée par le disque du fond (facile à calculer car sa surface est plane et horizontale)
La force de pression exercée par l'air atmosphérique
La force de pression exercée par la paroi tronconique : force inconnue mais facile à obtenir à partir de la condition d'équilibre de l'eau.
Le principe des actions réciproques (principe de l'action et de la réaction) permet d'affirmer que la force exercée par l'eau sur la paroi tronconique est l'opposée de la force exercée par la paroi tronconique sur l'eau.
Cela est un peu subtil mais évite tout calcul compliqué.
Un raisonnement analogue appliqué au récipient complet permet ensuite d'obtenir la force exercée par l'eau sur la calotte sphérique.
Bonjour vanoise,
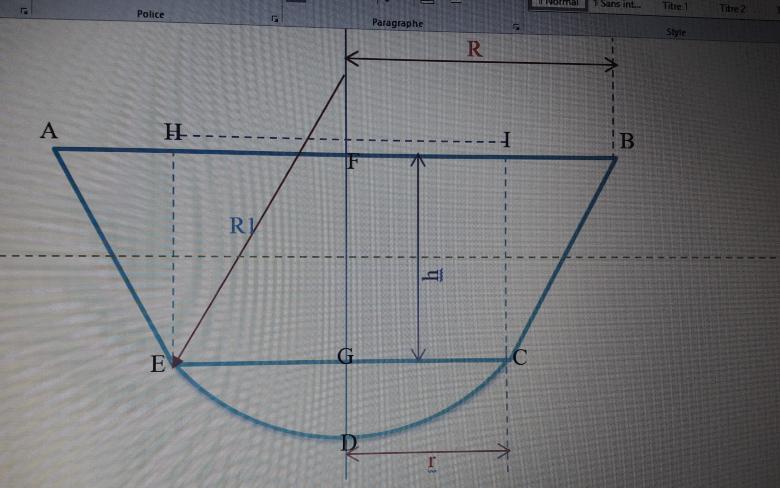
je reviens vers toi avec cette réponse pour la question 1(Calculer la poussée totale sur le fond ) , si tu peux vérifier mon raisonnement stp ( j'ai réalisé un schéma afin de voir les choses plus claires) .
Cherchons le rayon R1 de la sphère correspondant à la calotte sphérique constituant le réservoir.
EG² = GD( 2 R1 - GD),
Où :
r²= R1 /5 (2R1 - R1/5)
R1 = 5r/3
La poussée sur le fond sera égale au poids du liquide contenu dans le cylindre H E C I , plus le poids du liquide contenu dans le segment sphérique EDC , avec :
Poids du cylindre :
π r² hϖ
avec ϖ= ρ g = 1000 x 9.81= 9810 N
π 3²* 3*1000*9.81= 832113
Poids du segment sphérique :
(π )/(3 ) R1²/25 (3R1-R1/5)ϖ
où
(π )/(3 ) (25 r²)/25x9 (15r/3-r/3)ϖ
= (14πr )/81 ϖ
= (14π3 )/81 9810= 143822
La poussée sur le fond est = 832113+ 143822 = 975935 N
Bonjour
Tu as bien progressé en physique depuis l'époque où tu as posé ce premier message !
Je viens de vérifier ton raisonnement et tes calculs littéraux : pas de problème !
Pour les applications numériques, tu as raison de conserver un maximum de chiffres significatifs dans les calculs intermédiaires pour éviter que trop d'arrondis successifs finissent pas provoquer des erreurs. Cependant, le résultat final doit théoriquement être fournis avec autant de chiffres significatifs que n'en comporte la donnée la moins précise de l'énoncé... La difficulté ici est que le concepteur de ton énoncé ne se préoccupe guère de cela, fournissant 3 chiffres significatifs pour certaines données, 2 pour d'autres, un seul parfois... Dans ces conditions, je te conseille de fournir trois chiffres significatifs, ce qui donne ici : 9,76.105N .
Tu as bien compris comment te passer de calcul intégral pour déterminer les poussées. J'ai bien peur qu'un tel calcul soit inévitable pour déterminer la position du centre de poussée...
Le centre de poussée est demandé pour le fond uniquement.
Il me semble qu'en raison de la symétrie ...
Bonjour vanoise ....merci pour ton encouragement.....oui c'est vrai au début c'était un peu dur. ..Comme après le bac j'ai poursuivi des études de gestion et par la suite une expérience professionnelle de 12 ans... Or me voila aujourd'hui je recommence des études en ingénierie (mais à distance) ..C'est pour cela c'était un peu difficile au début.....
Votre forum est vraiment très utile et intéressant ...sincèrement ça m'a beaucoup aidé ...
surtout toi vanoise..je te remercie beaucoup..
Sans oublier le grand chef J-P ..qui est toujours là pour nous..
Bon revenant à notre exercice .. je suis contente que mon calcule pour la poussée sur le fond soit correct alors..
il me reste à calculer la poussée sur la paroi tronconique , lorsque le réservoir est plein d'un liquide de poids volumique ϖ et aussi déterminer la position du centre de pression sur le fond. ...je vais essayer de répondre dans le prochain message ....
merci encore une fois
Pour le centre de poussée, puisque l'énoncé se limite effectivement à la partie inférieure en forme de calotte sphérique, il suffit de se rappeler la définition du centre de poussée et de réfléchir aux directions des forces élémentaires de pression. La détermination du centre de poussée sur l'ensemble serait plus "calculatoire".
Pour la force de poussée sur la partie tronconique : surtout ne change pas une méthode qui gagne ! Relie éventuellement mes premiers messages. Puisque tu as déjà calculé le volume de la partie tronconique et celui du fond, tu peux assez facilement calculer le poids total d'eau... La réponse à la question précédente te permet alors très simplement d'aboutir...
Je te laisse réfléchir...
Bonsoir nano21
Ton raisonnement précédent est correct ainsi que les calculs mais tu n'es pas encore très à l'aise avec l'écriture des formules littérales...
Par exemple, l'avant dernière expression du poids d'eau dans le fond en forme de calotte sphérique (pas de segment circulaire) est correcte mais tu as oublié un cube dans la dernière expression : étourderie certainement puisque l'application numérique est correcte. Pour que tu continues sur de bonnes bases , je précise quelques résultats que tu as d'ailleurs déjà obtenus en ordre plus ou moins dispersé :
Volume du « fond » :
Poids d'eau dans cette partie :
Volume de la partie tronconique :
Poids d'eau dans cette partie :
Je te laisse gérer le nombre de chiffres significatifs et terminer ...
Bonjour vanoise ,
Merci pour ta réponse.
donc la poussée totale exercée par le liquide sur la paroi tronconique sera:
Pt+( (1/2 p g h) (Pi r²h)) ?
Bonjour
Quand tu as écris dans ton message précédent cette phrase :
La poussée sur le fond sera égale au poids du liquide contenu dans le cylindre H E C I , plus le poids du liquide contenu dans le segment sphérique EDC
j'ai crû que tu avais tout bien compris, même si l'expression "segment circulaire" n'est pas adaptée ici.
Tu peux appliquer un raisonnement analogue en considérant que la poussée exercée par l'eau sur le récipient entier (partie tronconique plus fond en forme de calotte sphérique) est le poids total de l'eau que tu connais. Ayant déjà calculé la poussée exercée sur le fond, par simple différence, tu auras ton résultat !
Remarque 1 : comme dans la plupart des problèmes de ce genre, je néglige l'influence de la pression atmosphérique dans la mesure où son action sur la surface libre (AB) de l'eau est compensée par l'action de la pression atmosphérique sur les parois du réservoir.
Remarque 2 : il est aussi possible d'obtenir le résultat par un calcul intégral comme expliqué dans mon message du 04-05-17 à 19:05. Ce calcul est nettement plus long et compliqué. Il n'est donc pas conseillé lorsque l'énoncé laisse comme ici le choix de la méthode. N'empêche : si tu as un peu de temps devant toi, tu pourrais peut-être essayer : j'ai vu des énoncés de problèmes où les deux méthodes étaient demandées...
Bonjour vanoise ...j'espère que tout va bien
je suis désolée du retard involontaire de ma réponse....
Nous avons :
Volume du « fond » :
Vf= 14p.r3 /81 = 14.66 m3
Poids d'eau dans cette partie :
Pf= p.Vf. g= 1,438.10^5 N
Volume de la partie tronconique :
Vt = pi.h /3 * (R²+r²+R.r) = 116,2 m3
Poids d'eau dans cette partie :
Pt= p.Vt.g= 11,40.105 N
• Poids du cylindre :
pi r² hϖ
pi 3²* 3*1000*9.81= 8,321. 10^5 N
donc
La poussée totale exercée par le liquide sur la paroi tronconique sera donc:
11,40.10^5 N + 1,438.10^5 N - 8,321.10^5 N
Bonjour
Le plus simple consiste à utiliser les résultats précédents :
Poussée totale de l'eau = poids total de l'eau ; soit , avec mes notation du 09-07-17 à 22:25 :
Pt+Pf
1,438.105+11,40.10512,84.105N
La question précédente avait permis de montrer que la poussée sur le fond vaut :
Pfond=9,759.105N
Par différence, la poussée de l'eau sur la partie tronconique vaut :
Ptc=Pt+Pf-Pfond3,082.105N
Valeur que l'on peut arrondir à 3,08.105N
Par rapport à ce que tu as fait : tu aurait dû soustraire le poids d'eau dans le cylindre et le poids d'eau dans le fond.
On arrive heureusement au même résultat par le calcul direct, calcul nettement plus compliqué...
Bonsoir Vanoise,
Si tu peux vérifier stp la position du centre de pression sur le fond:
Le centre de pression (points d'application de P1 et P2 ) est sur l'axe EC à une profondeur H donné par la formule :
Mi/Ms sur Oy= (Pi R^4/8) / ( Pi R²/2*4R/3Pi) = 3Pi R/16
Vanoise stp la formule relative au centre de pression est correcte?
D'où vient cette formule et comment la justifies-tu ?
Dans la mesure où il s'agit de déterminer le centre de pression ou centre de poussée des forces pressantes exercées par l'eau sur le fond uniquement en forme de calotte sphérique, aucune formule compliquée n'est nécessaire. Comme évoqué rapidement dans mon message du 09-07-17 à 15:21, il suffit de se rappeler la définition rigoureuse de ce point puis de réfléchir aux directions de ces forces de pression sur chaque portion élémentaire de surface de la calotte sphérique...
Je te laisse réfléchir...
Bonjour
vanoise je me suis trompée , j'ai appliqué une formule relative à un paroi demi-cercle ..
( mais je t'explique quand même:
on sait que CG=4R/3Pi
Mi= moment d'inertie du 1/2 cercle par rapport à son diamètre=1/2 moment d'inertie du cercle=PiR^4/8
donc Le centre de pression (points d'application de P1 et P2 ) est sur l'axe EC à une profondeur H donné par la formule :
Mi/Ms sur Oy= (Pi R^4/8) / ( Pi R²/2*4R/3Pi) = 3Pi R/16)
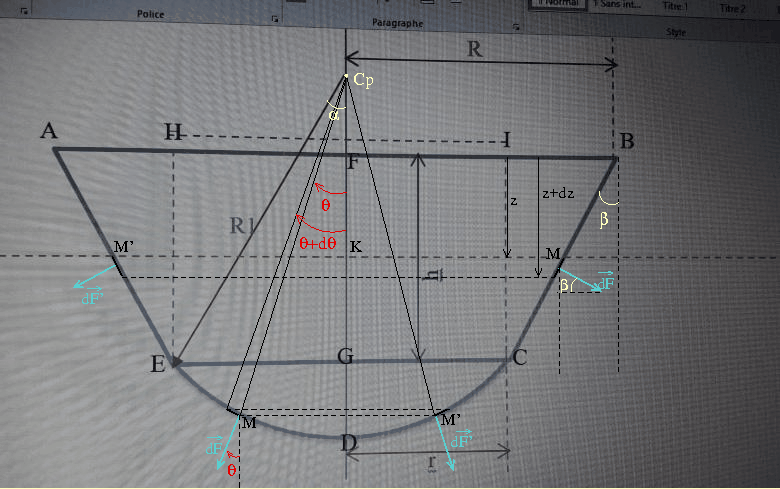
Les choses sont beaucoup plus simples dans ce cas particulier ! Il n'y a pas de formule compliquée à utiliser ; il suffit de connaître la définition du centre de poussée . Il s'agit du point, noté Cp, tel que le moment des forces pressantes en ce point est nul. Regarde le schéma ci-dessous : il a été fait pour illustrer le calcul direct possible (pas demandé ici) des forces de pression. Il est donc plus compliqué que nécessaire ici mais je n'ai pas le temps d'en refaire un autre. Soit un point M quelconque de la calotte sphérique entourée d'une surface élémentaire dS. La force élémentaire de pression exercée par l'eau sur cet élément de surface - de vecteur - est normale à cette surface élémentaire donc perpendiculaire au plan tangent en M à la calotte sphérique. Propriété simple des sphères : cette normale en M passe par le centre de la sphère. Le moment de cette force élémentaire au centre de la sphère est nul. Ce résultat est valide quelle que soit la position du point M sur la calotte sphérique. On peut donc affirmer que le moment des forces de poussées au centre de la sphère à laquelle appartient la calotte sphérique (le fond du récipient) est nul. Ce centre est donc le centre de poussée Cp !
De simples considérations géométriques permettent de positionner ce centre, par exemple en calculant la distance de F à Cp. Je ne suis pas sûr que le centre Cp soit parfaitement positionné sur la figure que tu as fournie et que j'ai reprise mais cette figure permet tout de même d'illustrer le raisonnement...
..la ligne d'action de la force passe par le centre de poussée qu'ont peut localiser en appliquant la formule:
yCP = distance au centre de poussée= (Icg/(ycg*A))+ ycg
où
Icg est le Moment d'inertie de la calotte par rapport à (Oz) ( avec La tranche de cote z et d'épaisseur dz a pour rayon : : r=R.sin(teta) et pour épaisseur dz= -R.sin(teta) )
=1/12 (p 
*R^5)
(Réaction rapide..je suis au bureau)
Réaction rapide..je suis au bureau
Effectivement : tu n'as pas pris la peine de bien lire et comprendre mon post précédent. Il est exact que l'on trouve dans la littérature des formules plus ou moins complexes faisant intervenir des moments d'inertie... Personnellement, dans les cas compliqués, je préfère repartir à zéro avec la formule du moment des forces. Mais ici, je me re-re-re-répète : puisque la surface sur laquelle s'exerce les forces de pression est une portion de sphère (peu importe d'ailleurs le "découpage" de la surface sur la sphère) et puisque, en statique des fluides, les forces élémentaires de pression sont en chaque point de la surface, normale à la surface, le centre de poussée est nécessairement le centre de la sphère puisqu'il s'agit du seul point où les moments des différentes forces élémentaires de pression est nul.
Réfléchis bien à tout cela : à la définition du centre de poussée, aux conditions pour lesquelles un moment de force est nul en un point.... Il est parfois plus compliqué de comprendre pourquoi il n'est pas nécessaire de faire un long calcul que d'appliquer une "formule"...
Tu n'as plus qu'à faire un simple raisonnement géométrique en tenant compte des données. En notant R1 le rayon de la sphère, l'énoncé précise :
R1=CpE=5.GD
CpG=4.R1/5
Sachant que r = h=3m, le théorème de Pythagore appliqué au triangle (CpEG) conduit à R1=5m ce qui conduit à FCp=1m
Le centre de poussée est sur l'axe de symétrie vertical du récipient, un mètre au dessus de celui-ci.
Annuler
connectez vous