Inscription / Connexion Nouveau Sujet
La masse d'un insecte sur l'eau
Bonjour, je viens à vous demander de l'aide pour cet exercice qui me parait vraiment compliqué. Je pense avoir compris qu'il faut calculer le volume d'eau déplacé par l'insecte( comme sur le schéma), et que cette masse d'eau déplacée correspondrait à la masse de l'insecte. D'une autre part, comme l'insecte a déjà 6 pattes, je me disais qu'il faut multiplier la masse d'eau déplacée par 6 pour avoir la masse totale de toutes les pattes.. Et obtenir la masse de l'insecte. Je ne sais par ailleurs pas comment mettre en application ce raisonnement.. Aidez moi svp
Un insecte à six pattes est posé sur l'eau.
Le rayon de la dépression circulaire formée
par chaque patte est de 1 cm et l'angle de
contact de 50°. Quelle est la masse de
l'insecte ?
Voici le schéma !
Voilà ce que j'ai compris :
La somme des forces donne l'équilibre : donc
le Poids de l'insecte+ F a force de tension = 0
Ensuite on remplace P par mg, et F par sa formule : F = σ x l
Ensuite je bloque T.T
Bonsoir,
Sur quel contour s'exerce ici la tension superficielle?
Comment représenter cette force sur le schéma?
F=2 l
l
Je veux bien, mais que vaut l ?
Pourquoi un facteur 2 ?
J'ai fait un schema qui taideras peut etre a mieux saisir la situation physique
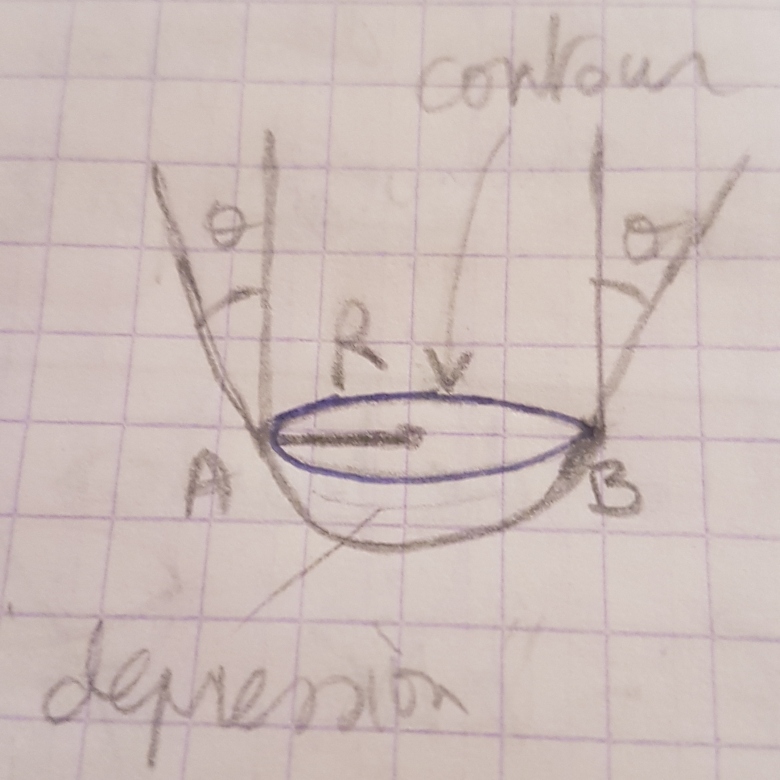
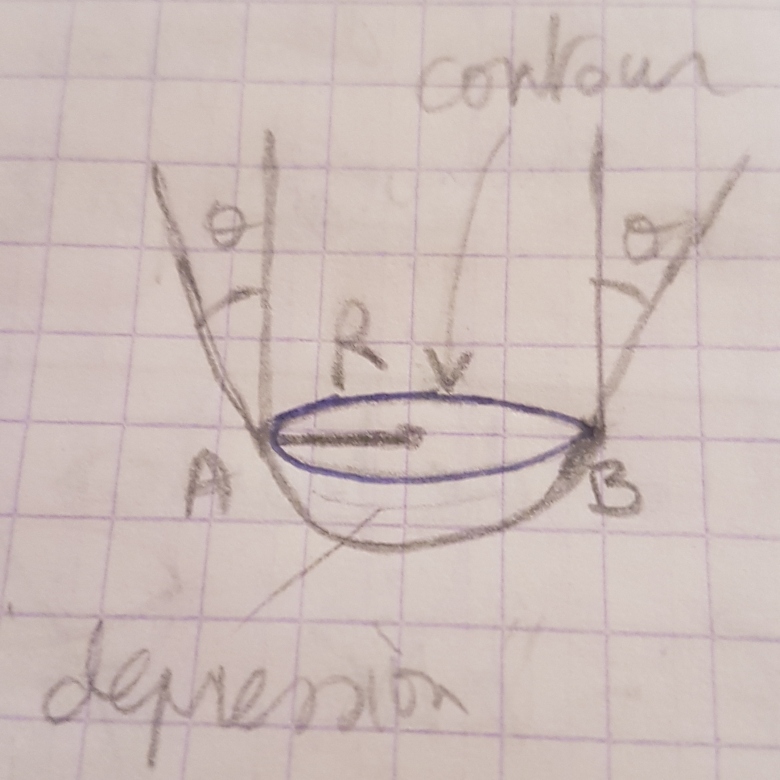
Bonsoir ! Merci pour ta réponse !
Tu as raison, l n'est pas égale à 1 cm. Je me suis trompée.
"l" sera égal à un arc de cercle : l = 2 x r x sin(50°/2)
Le facteur 2 correspond aux deux faces de la patte posée..non?
On ne considère que le contour qui délimite la dépression, et qui est circulaire (en bleu)
D'autre part quelle est la direction de dF, tension superficielle en A ? en B ?
F1 +F2 + P ( de l'insecte) = 0 à l'équilibre, puis on a F1=F2 donc on peut juste multiplier par 2 F1.
Puis, calculer l'intensité de P pour déduire m?
La tension superficielle se calcule sur un contour
dF=  dl
dl
Ici comment est dirigée la force dF en A ?
Cette force agit sur TOUT le contour, mais par symétrie ici on trouve très vite la composante verticale de Fz=  dFz
dFz
(horizontalement la résultante des forces de tension est nulle)
Je suis si nulle en physique.. Je dois rendre ce TD après les vacances mais je me sens pas avancer T.T
La formule est: dF =  dl
dl
Mais il faut aussi savoir que dF est tangente a la surface de leau et normale au contour en chaque point
Donc ici en A, dF est normale au cercle bleu et tangent a la surface de l eau en A donc il est comme sur la figure ci dessous, non?
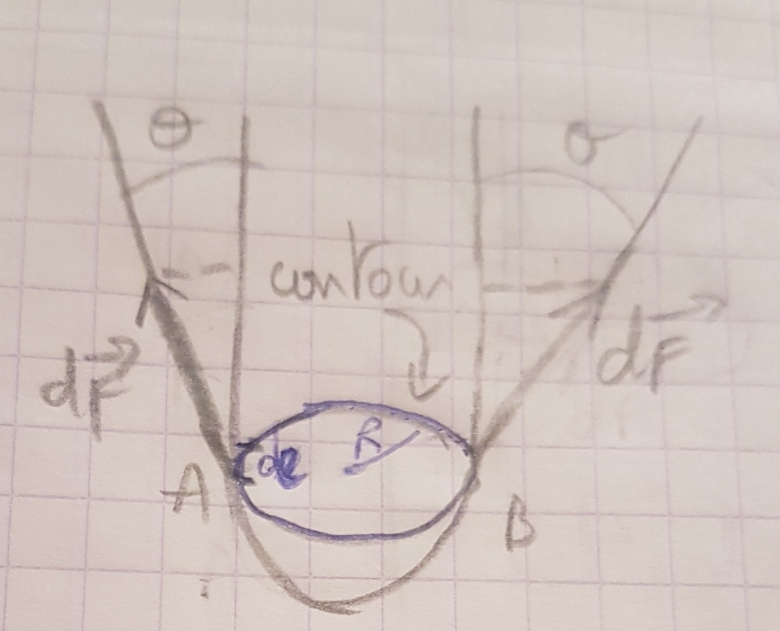
Faut dire que mes dessins sont très laids ! 
Donc que vaut la composante verticale dFz en A? en B ?
Et en fait par symétrie en chaque point du contour?
Et enfin que vaut Fz qd on intègre sur le contour?
Pour faire un tel exo il faut savoir intégrer une force infinitésimale sur un contour, même si ici c'est immédiat
dFz = dF cos  =
=  dl cos
dl cos 
Fz =  contour dFz =
contour dFz = 
 cos
cos  dl=
dl=  cos
cos 
 contour dl= 2
contour dl= 2 R
R  cos
cos 
Et finalement a l'équilibre de l'insecte: mg = 6 Fz
Je vous aime. C'est incroyable comme vous m'avez aidée là.. Je vous remercie mille fois <3<3<3<3<3<3<3 !!!!
Bonsoir ! je suis sur un exercice, voici l'énoncé :
Quelle est la valeur maximale de l'arête d'un cube de masse volumique ρ pour qu'il puisse
rester en flottation à la surface d'un liquide de masse volumique ρ0 inférieure à ρ ?
Je suis en train de le faire, mais si quelqu'un a une idée je suis preneuse 
Merci !
*** message déplacé ***
Bonjour,
C'est le même raisonnement qu'avec l'insecte mais avec un autre contour.
*** message déplacé ***
Bonjour à vous deux,
HamsterLife : pourrais-tu utiliser au maximum les possibilités offertes par le site pour les formules en lieu et place de photos de manuscrits :
Très bien ! Désolée je ne me suis pas encore familiarisée avec les symboles du forum !
Je vais m'y faire 
Cette solution correspond à un cube qui reste hors de l'eau.
Mais peut-on imaginer une situation où le cube serait immergé et "retenu par le haut" ?
Auquel cas on profiterait aussi de la poussée d'Archimède !
C'est une idée comme ca, je ne sais pas si c'est réalisable.
Très compliquée pour moi Haha !
Je pourrais demander ton aide pour un exercice que je viens de poster stp? 
Merci bcp !! 
Très compliquée pour moi Haha !
Non, il suffirait d'ajouter la poussée d'Archimède dans le bilan des forces.
Mais tu verras bien à la correction ce que le prof dira






 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
