Inscription / Connexion Nouveau Sujet
La guitare
Bonjour,
Sur un problème sur la corde de guitare , on demande de justifier pourquoi la surpression perçue est p(t) = p0(t) + p1(t) avec p0(t)= Acos(2*pi*f0t) et p1(t) = Acos(2*pi*f1t) lorsque les notes sont jouées en même temps.
Puis on demande de calculer p(t) et d'exprimer Tb en fonction de T1(associée à p1(t))et T0(associée à p0(t))
J'ai trouvé par linéairisation du cos que Tb=2T1T0/(T1+T0)
Mais j'arrive pas à en deduire comment le musicien détermine à l'oreille si la corde est accordée ou pas et comment il sait si il l'accorde ou pas
Bonjour
Est-il précisé dans l'énoncé si les deux fréquences fo et f1 sont de valeurs proches ?
Si oui, il s'agit d'un phénomène de battement ; en effectuant la somme des deux cosinus comme tu l'as fait, tu montres que la fréquence perçue est la moyenne des fréquences mais tu montres aussi que l'amplitude varie lentement au cours du temps. Cette lente variation de l'amplitude disparaît si fo=f1.
Oui f0 et f1 sont proches mais je ne vois pas comment on peut expliquer que c'est une somme et non la moyenne ou quoi que ce soit ? Si ce sont des battements comment le musicien le perçois quand c'est mieux accordé ?
Voila qui est plus clair !
Les pressions sont des grandeurs scalaires dont les effets s'ajoutent. Si une oreille est soumise à l'influence de deux sources sonores qui, séparément, produiraient au niveau du tympan les pressions acoustiques po(t) et p1(t), elle est soumise à la pression acoustique :
p(t)=po(t)+p1(t)
IL me semble préférable de raisonner sur les fréquences plutôt que sur les périodes.
Pour des fréquences proches, cela correspond à un signal sonore de fréquence égale à la moyenne des fréquence dont l'amplitude est la fonction du temps suivante :
Cette amplitude varie périodiquement très lentement entre zéro et 2A, ces maximums de 2A étant obtenues à la fréquence de battement :
Pour accorder un piano à partir de la note la3 (fréquence théorique 440Hz), on joue la note au piano tout en excitant un diapason qui émet un son pur de fréquence fo=440Hz. Si le piano est parfaitement accordé : f1=fo, l'accordeur entend un son de fréquence fo :
Si le piano n'est pas parfaitement accordé, il perçoit un son de fréquence égale à la moyenne des deux fréquence dont l'amplitude augmente puis diminue périodiquement à la fréquence fb. Il faut alors régler le piano jusqu'à faire disparaître ce phénomène de battement. Pour illustrer cela, voici la courbe p(t) (échelle arbitraire) pour fo=440Hz et f1=430Hz.
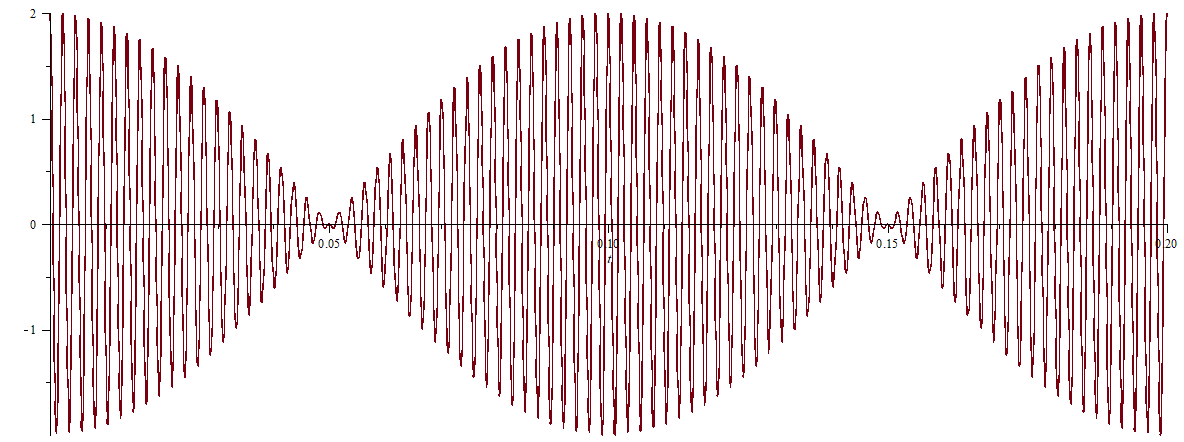
Merci bcp Vanoise votre réponse est très clair. Ainsi si on écoute la période des battement on peut aussi donc deviner si on accorde ou désaccorde .
Je voulais aussi savoir si vous pouvez m?aider pour les questions***lien supprimé****j?ai des difficultés avec les développements de fourrier et le mouvement de la corde
Le règlement du forum demande de recopier l'énoncé ou de le copier- coller puis d'expliquer ce que tu as fait et ce qui te bloque.
Ah d'accord donc on pince la corde mi à 1/5 de sa longueur et on la lache sans vitesse initiale . On neglige encore la raideur . On donne l'expression d'un mode propre de la forme : yn(x,t) = an sin(n  X/L) cos(n
X/L) cos(n ct/L)
ct/L)
On demande l'expression générale de y(x,t) je pense que c'est la serie des yn et cette vibration est-elle harmonique je ne vois pas ensuite on dit que y(x,0) peut s'écrit comme un développement de fourrier mais comment?
D'après le théorème de Fourrier, y(x,t) est la somme des yn(x,t) pour n variant de 1 à l'infini.
Tu peux alors dériver par rapport à t pour obtenir la vitesse y'(x,t). Tu obtiens les valeurs de en écrivant que la vitesse en t=0 est nulle pour tous les points de la corde.
Ensuite, il faut écrire que la forme initiale de la corde caractérisée par :
correspond au profil fourni correspondant à deux segments de droites. C'est là qu'intervient le développement de Fourrier qui peut aussi se transposer à la variable x.
Ah merci beaucoup si j'ai bien compris mais cette modélisation est elle inexacte si la corde serait raide sinon on aurait pas deux droites mais une sorte d'hyperbole ?
Mais voir que la série correspond à deux droites ce n'est pas évident du tout comment sans intuition physique mais mathématique cela aurait on pu le voir?
Je ne suis pas un guitariste émérite mais tout de même : pour "jouer" une note, il s'agit bien d'écarter transversalement la corde de sa position d'équilibre avec le doigt ou un accessoire (médiator) puis de lâcher la corde sans vitesse initiale. Bien sûr, l'extrémité du doigt n'est pas tout à fait ponctuelle et l'aspect de la corde à l'instant où on la lâche présente un léger "arrondi" en x=L/5. Cependant, la modélisation que l'on obtient ainsi est plutôt convenable dans la mesure où cette théorie est en très bon accord avec le spectre sonore obtenu expérimentalement.
Je te laisse finir le calcul :
avec f(x) définie “par morceaux” :

 n=0
n=0  n , le cas particulier t=0 conduit à :
n , le cas particulier t=0 conduit à :

