Inscription / Connexion Nouveau Sujet
la fibre optique
Bonjour,
Je suis sur un problème et je voulais votre avis.
"On considère, dans le vide, une fibre optique rectiligne, constituée de deux milieux transparents isotropes et homogènes: le cœur, d'indice n1 est un cylindre d'axe (Oz) et de rayon a et la gaine entourant le cœur, d'indice n2<n1 est limitée par un cylindre de même axe (Oz) et de rayon b.
Un rayon lumineux (S) monochromatique de longueur d'onde  atteint le cœur de la fibre au point O, avec l'angle d'incidence
atteint le cœur de la fibre au point O, avec l'angle d'incidence  et donne un rayon réfracté (S1) dans le cœur de la fibre.
et donne un rayon réfracté (S1) dans le cœur de la fibre.
On donne n1=1,456 et n2=1,410
1)Indiquer la condition que doit remplir l'angle  pour que le rayon (S1) subisse une réflexion totale sur la surface de séparation entre le cœur et la gaine, en faisant apparaître un angle limite
pour que le rayon (S1) subisse une réflexion totale sur la surface de séparation entre le cœur et la gaine, en faisant apparaître un angle limite  0. On appelle
0. On appelle  l'ouverture numérique de la fibre définie par
l'ouverture numérique de la fibre définie par  =sin
=sin 0. Calculer numériquement
0. Calculer numériquement  .
.
2)Quel est l'intérêt de vérifier la condition de réflexion totale? Représenter le rayon (S) et les aryons dans la fibre; sont-ils tous dans le même plan?
On se place désormais dans le cas où l'incidence conduit à une propagation sans pertes.
3)Exprimer la vitesse de propagation de la lumière dans la fibre en fonction de c, la vitesse de la lumière dans le vide et de n1. Pourquoi utilise-t-on des sources monochromatiques?
4)Le rayon (S) est le support d'un signal lumineux de la forme d'une très brève impulsion, qui est émis à l'instant t=0 au point O et se propage le long de la fibre. Montrer que la durée de parcours  de la lumière dans la fibre de longueur L dépend de l'angle d'incidence
de la lumière dans la fibre de longueur L dépend de l'angle d'incidence  sur la face d'entrée. Exprimer
sur la face d'entrée. Exprimer  en fonction de n1, L, c et
en fonction de n1, L, c et  .
.
5)Le signal est maintenant porté par un ensemble de rayons convergeant en o avec 0< <
< 0. Montrer que l'impulsion émise à t=0 est alors élargie lorsqu'elle est transmise le long de la fibre. Calculer la différence
0. Montrer que l'impulsion émise à t=0 est alors élargie lorsqu'elle est transmise le long de la fibre. Calculer la différence 
 entre la durée maximale et la durée minimale de propagation d'un bout à l'autre de la fibre. Application numérique pour L=1,00km.
entre la durée maximale et la durée minimale de propagation d'un bout à l'autre de la fibre. Application numérique pour L=1,00km.
6)Le signal transporté par la fibre est constitué d'impulsions lumineuses d'une durée T1 à intervalle régulier T. Quelle valeur minimale T faut il choisir pour que les impulsions soient distinctes à la sortie de la fibre? Proposer une définition de la bande passante en bits (nombre d'impulsions par secondes. Comparer la valeur de la bande passante obtenue ici avec celle d'un téléphone portable (64bits par seconde) et celle de la télévision (100 Mbits par seconde)."
1)Une réflexion totale sur la surface de séparation entre le cœur et la gaine est possible comme n1>n2. Il faut que l'angle d'incidence du rayon sur ce dioptre, noté i, vérifie |sini|>n2/n1. De plus,  =r-
=r- /2 avec r l'angle de réfraction de l'entrée du rayon dans le cœur, donné par la loi de Descartes: n1sinr=nairsin
/2 avec r l'angle de réfraction de l'entrée du rayon dans le cœur, donné par la loi de Descartes: n1sinr=nairsin
On a alors |sini|=cosr=sqrt(1-sin^2r)=sqrt(1-(nairsin /n1)^2)
/n1)^2)
La condition de réflexion totale:
nair^2*sin^2 /n1^2<1-n2^2/n1^2, càd -
/n1^2<1-n2^2/n1^2, càd - 0<
0< <
< 0
0
avec  0=arcsin(sqrt(n1^2-n2^2)/nair)
0=arcsin(sqrt(n1^2-n2^2)/nair)
On a  =sin
=sin 0=sqrt(n1^2-n2^2)=0,363
0=sqrt(n1^2-n2^2)=0,363
2)"croquis"
Je ne sais pas quel est l'intérêt de la réflexion totale mais les rayons sont dans le même plan.
3)v=c/n1
La vitesse de propagation dans un milieu transparent dépend de la longueur d'onde dans le vide. Ainsi les différentes composantes d'un signal lumineux ne se propagent pas à la même vitesse. On choisit une source monochromatique pour éviter le phénomène de dispersion.
4)Là je bloque.
5) Le temps le plus court est celui obtenu en se déplaçant sur l'axe. On obtient comme valeur Ln1/c. Le temps le plus long correspond à l'angle limite  0, càd Ln1/c*cosi; On en déduit
0, càd Ln1/c*cosi; On en déduit 
 =Ln1/c((1/cosi)-1).
=Ln1/c((1/cosi)-1).
Pour L=1,00km, on trouve 
 =0,158
=0,158 s.
s.
6)Il faut que T>
 soit f<1/
soit f<1/
 =
= f=6,3*10^6 bits par seconde. La fibre ne convient pas pour la TV mais convient pour le téléphone."
f=6,3*10^6 bits par seconde. La fibre ne convient pas pour la TV mais convient pour le téléphone."
Qu'en dites vous? Pouvez vous me donner des pistes pour les passages où je bloque? Merci!
Bonsoir parrax,
des exercices sur la fibre optique, il y en a des brouettes sur le forum ainsi que sur internet. Une recherche avec le moteur de recherche de l'île de la physique (voir en haut et à gauche de cette page) t'aurait fait gagner du temps. Tu peux aussi consulter le topic suivant (clique sur la maison), auquel j'ai répondu il y a longtemps, et qui peut-être t'aidera : ![]() Optique géométrique .
Optique géométrique .
1)
OK, Je trouve comme toi.
2)
Si il y a réflexion totale, le rayon entrant arrivera sans atténuation en sortie de la fibre.
Si il n'y a pas réflexion totale, le rayon sort , au moins en partie, en dehors de la fibre. Il y a alors des pertes dans la fibre ... Le rayon en sortie est atténué par rapport au signal d'entrée.
3)
OK
4)
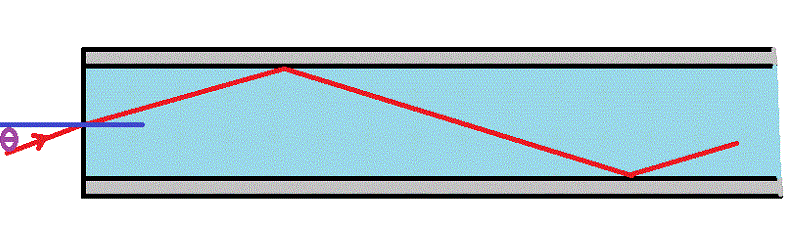
Sur le dessin, on voit bien que la distance parcourue par le rayon (que j'ai dessiné en rouge) est plus grande que la longueur de la fibre (du moins pour theta différent de 0°)
Comme tu as bien répondu à la question 1, tu devrais arriver (grâce aux angles) à calculer le rapport entre la longueur en rouge sur mon dessin et la longueur L de la fibre ...
Je n'ai pas eu le courage de lire plus loin ...



