Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 3 +

Niveau licence
Partager :

La bouée qui danse

Posté par
Jawad0610 09-04-20 à 06:03

Bonjour à tous ,

Voici un énoncé que l'on me propose:

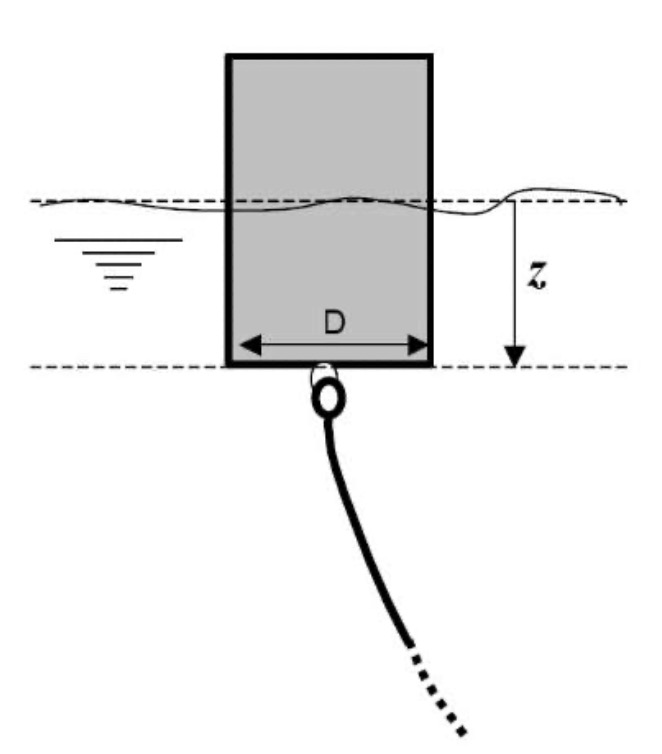
Une bouée d'amarrage cylindrique flotte à la surface de l'eau (voir schéma ci-dessous). Sous l'action des mouvements de houle, la bouée peut se mettre à osciller suivant un mouvement vertical.
Nous vous proposons dans cet exercice de mettre en équation le comportement dynamique de cette bouée.
Nous supposerons que la chaine reliant la bouée à son ancre n'est pas tendue. L'action de tension de la corde sur la bouée sera donc négligée.

Données :
Masse volumique de l'eau de mer : 𝜌􏰕 = 1026𝑘𝑔/𝑚􏰖3
Diamètre de la bouée : 𝐷 = 1,35𝑚
Masse de la bouée : 𝑀 = 1250𝑘𝑔
Accélération de la pesanteur : 𝑔 = 9,81 𝑚/𝑠􏰗2
On note z la distance de la surface inférieure de la bouée à la surface de l'eau

1) Etablir le bilan des efforts exercés sur cette bouée en absence de houle.

2) En déduire la hauteur de bouée immergée h0 à l'équilibre statique.

3) On néglige dans un premier temps les forces de frottement exercées par l'eau sur la bouée. Le plongeur
de l'exercice précédent s'est amusé à tirer verticalement sur la chaine sous la bouée et la lâche sans vitesse initiale. On note z1 la hauteur immergée de la bouée à l'instant où le plongeur relâche la corde (on prendra cet instant comme instant initial t=0). Déterminer l'équation de mouvement de la bouée (ne pas la résoudre dans cette question).

4) Montrer que cette équation de mouvement peut s'écrire sous la forme : M\ddot Z + kZ = 0
Vous préciserez l'expression du paramètre de position Z de la raideur équivalente k de cet oscillateur à un degré de liberté.

5) En déduire la fréquence propre de ce système oscillant.

6) Déterminer la force que doit exercer le plongeur pour déplacer la bouée de 2cm par rapport à sa position
d'équilibre statique.

La force résistive de frottement visqueux exercée par l'eau sur la bouée peut être approchée par l'expression \vec{F_v} = -p_0SC\vec{v} où S est la section de la face inférieure de la bouée, C un coefficient de viscosité surfacique et 𝑣⃗ la 􏰘􏰕
vitesse verticale.

7) Ecrire l'équation sur Z du mouvement libre vertical de la bouée en prenant en compte cette force résistive.

8) On donne 𝐶 = 35𝑚s-1. En déduire le régime des oscillations libres de la bouée.

9) Déterminer l'expression du déplacement Z(t) en fonction des conditions initiales.

10) Quelle période de houle peut faire entrer cette bouée en résonance ?

La bouée qui danse

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 06:11

Pour la question 1:

En absence de houle, on a:

-Le poids: P = Mg

-La poussée d'Archimède: P_A = - p_0gV_i avec Vi le volume immergé de la bouée.

On a :

V_i = \pi \frac{D^2}{4} z

Donc  P_A = - p_0g \pi \frac{D^2}{4} z

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 06:17

Pour la question 2:

D'après la deuxième loi de newton, à l'équilibre statique on a:

Mg = p_0g \pi \frac{D^2}{4} h_0

h_0 = \frac{4M }{p_0 \pi D^2}

h_0 \approx 0,85 m  

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 06:17

Est-ce bien correct?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 09:35

Bonjour
Oui : bon courage pour la suite !

Posté par
vanoisere : La bouée qui danse 09-04-20 à 10:32

Juste une remarque complémentaire sur la précision des résultats. La règle usuelle demande d'arrondir les applications numériques avec autant de chiffres significatifs qu'il y en a dans la donnée la moins précise de l'énoncé. Il faudrait donc arrondir dans ce problème à 3 chiffres significatifs : ho0,851m.
Attention à bien conserver en mémoire de la calculatrice tous les chiffres significatifs ; sinon, les arrondis successifs, dans un problème assez long, risquent d'induire des erreurs non négligeables.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 13:45

D'accord, merci pour votre remarque. Je vais continuer à avancer, je posterai un message sous peu.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 16:56

Pour la question 3:

Je comprends bien que dans ce genre d'exercices, on nous demande d'exprimer la hauteur à l'équilibre pour pouvoir l'utiliser dans la détermination de l'équation différentielle.

Je voudrais juste savoir:

Est-ce que z1 = h0 ?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 17:15

Citation :
Est-ce que z1 = h0 ?

Non !  La bouée étant à l'équilibre (z = h1), on tire sur la corde de façon à enfoncer la bouée d'une hauteur supplémentaire (2cm selon la question 6). A cette profondeur z1  supérieure à ho , la poussée d'Archimède est plus intense que le poids ; quand le plongeur lâche la corde, la bouée remonte mais, à cause de son inertie, elle monte plus haut que sa position d'équilibre ; le poids devient alors supérieur à la poussée d'Archimède ; la bouée s'enfonce à nouveau et ainsi de suite. La bouée va se mettre à osciller verticalement autour de sa position d'équilibre. La profondeur quelconque à la date t au cours de ces oscillations peut s'écrire sous la forme :
z=ho + Z;
Z désigne donc la variation de profondeur par rapport à la position d'équilibre. Ce changement de variable va te permettre, en tenant compte de la condition d'équilibre que tu as déjà obtenue, d'obtenir l'équation différentielle simple donnée question 4).

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 17:32

Le fait que l'on nous donne z1 m'a perturbé dans mon choix pour le changement de variable, je pensais qu'il fallait que j'utilise z1.

Pour la 3, j'ai donc:

h_0 = \frac{4M}{p_0 \pi D^2}

z = Z + h0

En appliquant la première loi de Newton, j'ai:

M \ddot z = Mg - \frac{p_0 g \pi D^2}{4}z

M \ddot Z = Mg - \frac{p_0 g \pi D^2}{4}(h_0+Z)

M \ddot Z = Mg - \frac{p_0 g \pi D^2}{4}(\frac{4M}{p_0 \pi D^2}+Z)

M \ddot Z = Mg - Mg - \frac{p_0 g \pi D^2}{4}Z

M \ddot Z + \frac{p_0 g \pi D^2}{4}Z = 0

Je me demande juste, où faudrait-il que je m'arrête pour la question 3?

Car, ce que j'ai à faire pour la question 4, c'est poser:

k = \frac{p_0 g \pi D^2}{4}

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 17:35

Aussi, je n'ai pas bien compris ce que l'on me demande de faire ici:

Jawad0610 @ 09-04-2020 à 06:03

Vous préciserez l'expression du paramètre de position Z de la raideur équivalente k de cet oscillateur à un degré de liberté.

Posté par
vanoisere : La bouée qui danse 09-04-20 à 17:58

La question 3 s'arrête après cette ligne que tu as écrite :
M \ddot z = Mg - \frac{p_0 g \pi D^2}{4}z . Inutile à cette question de définir Z.
Question 4 : tu expliques alors que, pour simplifier, tu choisis une nouvelle origine des profondeur, non plus à la surface libre de l'eau mais à la position d'équilibre. Ainsi : Z=z-ho . La justification de l'expression de Z se fait donc à cette question 4, et tu obtiens , comme tu l'as très bien fait, la bonne équation différentielle vérifiée par Z , puis l'expression de k.
Mon message de 17h15 avait pour but de te donner la méthode générale mais ne respectait pas tout à fait l'ordre des questions posées.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 18:03

D'accord, merci pour ces remarques.

Quant à cela:

"Vous préciserez l'expression du paramètre de position Z de la raideur équivalente k de cet oscillateur à un degré de liberté."

Si je comprends bien, il faut que j'exprime Z en résolvant l'équation différentielle. Je vais m'atteler à cela.

Posté par
vanoisere : La bouée qui danse 09-04-20 à 18:18

Ne te prends pas trop la tête ! Au début de la question 4, tu justifie simplement le changement de variable en expliquant que la nouvelle origine des profondeur est prise à la position d'équilibre et non plus à la surface. Cela donne immédiatement :
Z=z-ho . Tu remplaces alors dans l'équation différentielle obtenue en 3) z par (Z+ho) et tu arrives à l'équation différentielle simplifiée. Cela donne tes équations déjà écrites :
M \ddot Z = Mg - \frac{p_0 g \pi D^2}{4}(h_0+Z) \\ \\ M \ddot Z = Mg - \frac{p_0 g \pi D^2}{4}(\frac{4M}{p_0 \pi D^2}+Z) \\ \\ M \ddot Z = Mg - Mg - \frac{p_0 g \pi D^2}{4}Z \\ \\ M \ddot Z + \frac{p_0 g \pi D^2}{4}Z = 0
Par identification, tu obtiens k. Ce que tu as également fait. Selon moi, tu peux passer aux questions suivantes !

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 18:33

J'ai quand même essayé ^^. On a:

M \ddot Z + kZ = 0

On note \omega_0^2 = \frac{k}{M}

\ddot Z + \omega_0^2Z = 0

D'après le cours, on a:

Z = Acos(\omega_0t) + Bsin(\omega_0t)

On utilise la position initiale:

Z(0) = z(0) - h_0 = z_1 - h_0 = A

On utiliser la vitesse initiale:

Aussi, on a:

\dot Z = -A\omega_0sin(\omega_0t) + B\omega_0cos(\omega_0t)

La bouée est lâchée sans vitesse initiale, donc v_0 = \dot Z(0) = 0 = B\omega_0

On a donc B = 0.

On a donc:

Z(t) = (z_1 - h_0)cos(\omega_0t)

Est-ce bien correct?

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 18:49

Pour la question 5:

On note f0 la fréquence propre.

D'après le cours, on a:

\omega_0 = 2 \pi f_0

f_0 = \frac{\omega_0}{2\pi}

On sait que: \omega_0 = \sqrt{\frac{k}{M}}

f_0 = \frac{ \sqrt{\frac{k}{M}}}{2\pi}

On sait que: k =\frac{p_0 g \pi D^2}{4}

\sqrt{k} =\frac{D \sqrt{p_0 g \pi}}{2}

f_0 = \frac{\frac{D\sqrt{p_0 g \pi}}{2\sqrt{M}}}{2 \pi}

f_0 = \frac{D\sqrt{p_0 g}}{4\sqrt{M}\sqrt{\pi}}

Est- ce bien correct?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 18:54

Tout ce que tu as écrit est correct mais, en relisant l'énoncé, j'ai l'impression que la résolution de l'équation horaire en absence de frottement n'est pas demandée. Il faut obtenir Z(t) uniquement à la question 9 en tenant compte des frottements. L'équation différentielle obtenue en 4 a seulement pour but d'introduire en 5 la notion de fréquence propre et de pulsation propre.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 18:54

D'accord.

Ai-je bien exprimé la fréquence propre?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 18:59

Citation :
Ai-je bien exprimé la fréquence propre?

Oui !

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 19:17

Pour la question 6:

On note F la norme de la force exercée par le plongeur.

Si on veut enfoncer la bouée de 2 cm supplémentaire:

Mg + F = p_0g\pi \frac{D^2}{4}(h_0+0,02)

F = p_0g\pi \frac{D^2}{4}(h_0+0,02)- Mg  

En faisant l'AN, j'ai: F = 2145 N

Est-ce bien correct?

Cela me paraît beaucoup pour un seul homme, après c'est vrai que la bouée a une masse de plus d'1 tonne.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 19:18

Je ne l'ai pas précisé, mais j'ai pris un axe vertical orientée vers le bas, c'est pourquoi les normes de P et F sont positives tandis que celle de la poussée d'Archimède est négative.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 19:20

J'ai fait une erreur dans l'AN, je oublié de multiplier par (h_0+0,02).

Je trouve donc:

F = 286N

Est-ce correct?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 19:31

D'accord avec ton dernier résultat. Le premier était effectivement totalement irréaliste.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 20:01

Pour la question 7:

On inclut la force résistive de frottement visqueux dans notre application de la loi de Newton:

On sait que z = h_0 + Z donc \dot z = \dot Z

M\ddot Z = -kZ - p_0SC\dot Z

M\ddot Z + p_0SC\dot Z + kZ= 0

\ddot Z + \frac{p_0SC}{M}\dot Z  \omega_0^2Z= 0

Je "réarrange l'équation" pour exprimer le taux d'amortissement.

\ddot Z + 2\frac{k}{M}\frac{p_0SC}{2k}\dot Z  \omega_0^2Z= 0

\ddot Z + 2\omega_0 \sqrt{\frac{k}{M}}\frac{p_0SC}{2k}\dot Z  \omega_0^2Z= 0

On note le taux d'amortissement:

\alpha =\sqrt{\frac{k}{M}}\frac{p_0SC}{2k}

\alpha = \frac{p_0SC}{2\sqrt{M}\sqrt{k}}

\alpha = \sqrt{\frac{M}{k}} \frac{p_0SC}{2M}

\alpha = \frac{p_0SC}{2M\omega_0}

Est-ce bien correcte?

Il faut que je travaille sur l'équation caractéristique.

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 20:27

Pour la 8:

On a exprimer l'équation du mouvement sous la forme:

\ddot Z + 2\alpha \omega_0 \dot Z + \omega_0^2 Z = 0

Comme polynôme caractéristique, j'ai donc:

r^2 + 2\alpha \omega_0 r + \omega_0^2 = 0

Pour le discriminant, on a:

\delta = (2\alpha \omega_0)^2 - 4 \omega_0^2

\delta = 4\alpha^2 \omega_0^2 - 4 \omega_0^2

\delta = 4\omega_0^2( \alpha^2 - 1)

Le signe du discriminant et donc le régime dépend du signe de .

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 20:27

Dépend du signe de (2-1) *

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 20:37

\alpha = \frac{p_0SC}{2M\omega_0}

S = \frac{\pi D^2}{4}

\omega_0 = \sqrt{\frac{k}{M}}

\sqrt{k} = \frac{D\sqrt{p_0g\pi}}{2}

\omega_0 =\frac{D\sqrt{p_0g\pi}}{2\sqrt{M}}

\alpha = \frac{p_0SC}{\frac{2M D\sqrt{p_0g\pi}}{2\sqrt{M}}}

\alpha = \frac{p_0SC}{D\sqrt{M}\sqrt{p_0g\pi}}

\alpha = \frac{p_0 D^2 \pi C}{4 D\sqrt{M}\sqrt{p_0g\pi}}

\alpha = \frac{DC \sqrt{p_0\pi} }{4 \sqrt{Mg}}

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 20:39

Je trouve \alpha \approx 6.07

On a donc (^2 - 1) > 0 et donc le discriminant est positif.

Le régime est donc sur amorti.

Est-ce bien correct?

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 22:31

Par contre, vous m'aviez dit que la bouée allait osciller autour de sa position d'équilibre. Or, j'ai comme résultat un régime sur amorti. Ce qui voudrait dire que la bouée revient à sa bouée d'équilibre sans osciller.

Y'a-t-il un problème dans mes calculs?

Posté par
vanoisere : La bouée qui danse 09-04-20 à 23:39

C'est vrai que, intuitivement, avant de faire les calculs, j'imaginais un régime pseudo périodique assez fortement amorti mais tout calculs faits, j'arrive au même résultat que toi. Avec les valeurs numériques de ton énoncé, il faut donc prévoir un régime apériodique.
Cela va poser un problème à la dernière question où il est question de résonance. L'énoncé n'est pas précis : résonance de vitesse ou résonance d'amplitude ? Si la résonance de vitesse existe quelle que soit la valeur de pour une fréquence d'excitation égale à la fréquence propre, la résonance d'amplitude n'existe que pour des valeurs de pas trop grandes (je te laisse faire éventuellement la démonstration) ; elle n'existe pas pour une valeur de égale à 6,06... Quand à la résonance de vitesse, elle sera extrêmement floue avec une valeur aussi élevée de ...
Je trouve la valeur de C particulièrement élevée. Une valeur 10 fois plus petite aurait conduit à =0,606 ; situation à mon avis beaucoup plus réaliste...

Posté par
Jawad0610re : La bouée qui danse 09-04-20 à 23:42

C'est aussi ce que je me suis dit, la valeur de C m'a l'air beaucoup trop élevée. J'ai envoyé un message à ma professeure, en espérant que j'obtienne une réponse rapidement. Je posterai un message dès que j'ai un retour.

Posté par
vanoisere : La bouée qui danse 09-04-20 à 23:45

OK : tant que tu y es : pose lui la question du type de résonance : résonance de vitesse ou résonance d'amplitude ? (Par défaut en mécanique, on parle en général de résonance d'amplitude mais autant être précis...)

Posté par
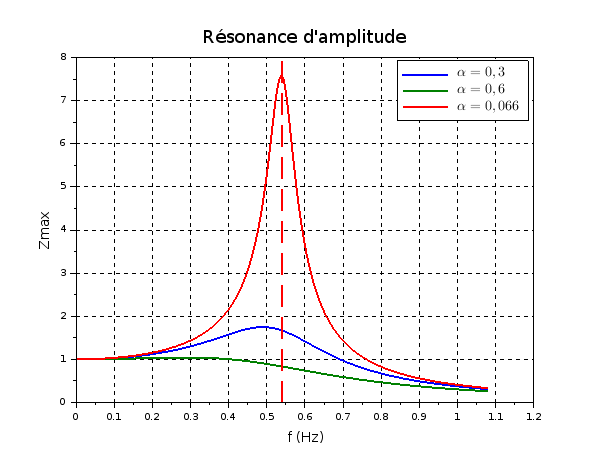
Jawad0610re : La bouée qui danse 09-04-20 à 23:50

C'est noté

Posté par
vanoisere : La bouée qui danse 10-04-20 à 14:56

Pour illustrer mes propos précédents concernant les résonances, je joins deux simulations. Il s'agit bien sûr d'une modélisation très simplifiée : je suppose que le niveau moyen de la mer varie sinusoïdalement à une fréquence f par rapport à un repère galiléen. Cela revient à remplacer dans l'équation différentielle Z par Z-H.cos(.t) et on cherche les solutions de la nouvelle équation différentielle en régime sinusoïdal établi en posant :
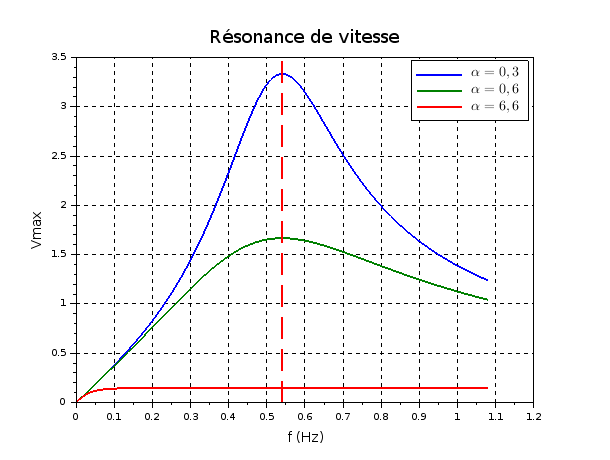
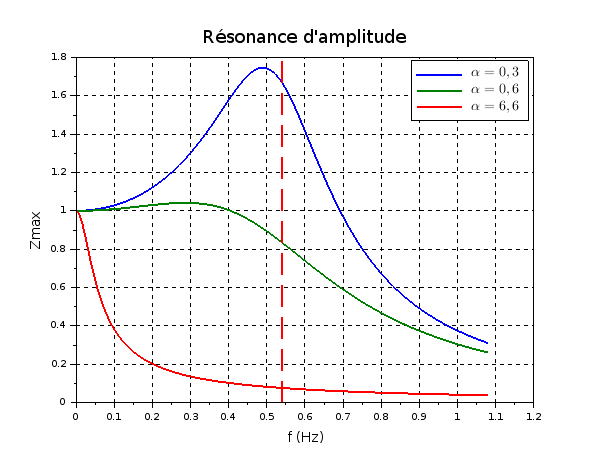
Z=Zmax.cos(.t-). Pas question de faire l'étude théorique dans le cadre de ce problème. Je fournis juste les résultats pour des fréquences variant autour de la fréquence propre. Vm désigne la vitesse maximale (celle en Z=0) et Zm l'amplitude des oscillations. Les échelles verticales sont arbitraires mais identiques pour les trois courbes.
On voit bien que pour =6,6, la résonance de vitesse est tellement floue qu'elle est en pratique indétectable. Pour cette valeur, la résonance d'amplitude n'existe pas.
Les tirets rouges verticaux ont pour abscisses f=fo.

La bouée qui danse

La bouée qui danse

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 17:56

Ma professeure a bien confirmé qu'il y a une erreur. Il faut prendre C = 0,35 m/s.

Pour la question 8, on a donc:

On a donc = 0,606.

Ainsi 2 - 1 <0, le discriminant est négatif et on a un régime sous amorti.

Est-ce bien cela?

Posté par
vanoisere : La bouée qui danse 10-04-20 à 18:23

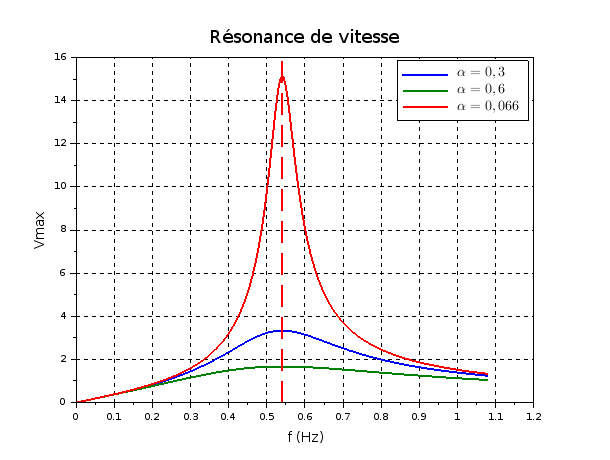
Par rapport à l'énoncé initial, diviser C par 100 divise aussi par 100, ce qui donne : =0,0606. Bien sûr : le régime est un régime pseudo-périodique : on peut décrire le mouvement comme un mouvement oscillatoire dont l'amplitude décroît exponentiellement mais très lentement compte tenu de la valeur de très petite devant 1. Une valeur aussi petite conduit à une résonance extrêmement aiguë comme le montre les courbes ci-dessous. Cela ne me parait pas non plus très réaliste (personnellement, j'aurais bien vu voisin de 0,3...) mais possède au moins un avantage. Tu peux considérer sans calcul que la résonance d'amplitude se produit à une fréquence extrêmement proche de la fréquence propre fo déjà calculée.

La bouée qui danse

La bouée qui danse

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 18:25

Pour la question 9:

D'après le cours, on peut écrire Z(t) sous la forme:

Z(t) = Ae^{-\alpha \omega_0 t} sin(\omega_d t + \phi)

D'après le cours, on a:

\omega_d = \omega_0 \sqrt{1-\alpha^2}

A = \sqrt{\frac{(v_0 + \alpha \omega_0 x_0)^2 + (x_0 \omega_d)^2}{\omega_d^2}}

\phi = artcan( \frac{x_0 \omega_d}{v_0 + \alpha \omega_0 x_0})

Posté par
vanoisere : La bouée qui danse 10-04-20 à 18:31

L'étude de l'amplitude et de la phase initiale ne semblent pas demandée ici mais la relation : \omega_d = \omega_0 \sqrt{1-\alpha^2} est tout à fait en accord avec mon message précédent et les courbes tracées : si 2<<1 :
d o

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 18:32

On a Z(t) = z(t) - h0

Pour la position initiale, on a:

x_0 = Z(0) = z(0) - h_0 = z_1 - h_0

Pour la vitesse initiale, on a:

On sait que le flotteur est lâché sans vitesse initiale, donc:

v_0 = \dot Z(0) = \dot z(0) = 0

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 18:34

vanoise @ 10-04-2020 à 18:31

L'étude de l'amplitude et de la phase initiale ne semblent pas demandée ici mais la relation : \omega_d = \omega_0 \sqrt{1-\alpha^2} est tout à fait en accord avec mon message précédent et les courbes tracées : si 2<<1 :
d o


Ne faut-il pas que je détermine l'expression de la phase initiale ?

Car on me demande de "Déterminer l'expression du déplacement Z(t) en fonction des conditions initiales."

Posté par
vanoisere : La bouée qui danse 10-04-20 à 18:47

Tu as raison ; j'en étais déjà à la dernière question. On demande effectivement Z(t). J'ignore les exigences de ton professeur et l'utilisation éventuelle de formulaires. Personnellement, je ne retiens pas les expressions des racines de l'équation caractéristiques et des conditions initiales :

\dot{Z}_{(0)}=0\quad;\quad Z_{(0)}=z_{1}-h_{o}

Il y a des simplifications en tenant compte de \alpha^{2}\ll1.

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 18:49

En remplaçant d par 0, en prenant en compte que v0 = 0 et que x0 =  z1 - h0, je simplifie les expressions des différents termes:

A = \sqrt{\frac{(\alpha\omega_0 (z_1 - h_0))^2 + ((z_1 - h_0)\omega_0)^2}{\omega_0^2}}

\phi = arctan(\frac{x_0\omega_0}{\alpha\omega_0 x_0}) = arctan(\frac{1}{\alpha})

Pour Z(t), j'ai donc:

Z(t) =\sqrt{\frac{(\alpha\omega_0 (z_1 - h_0))^2 + ((z_1 - h_0)\omega_0)^2}{\omega_0^2}}e^{-\alpha\omega_0t}sin(\omega_0t+ arctan(\frac{1}{\alpha}))

Z(t) =\frac{\sqrt{(\alpha\omega_0 (z_1 - h_0))^2 + ((z_1 - h_0)\omega_0)^2}}{\omega_0}}e^{-\alpha\omega_0t}sin(\omega_0t+ arctan(\frac{1}{\alpha}))

Est-ce bien correct?

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 18:51

Peut-on faire des simplifications supplémentaires?

Posté par
vanoisere : La bouée qui danse 10-04-20 à 19:12

Valeur approchée de arctan(1/) avec <<1 ?
On peut aussi obtenir une valeur approchée de l'amplitude.

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 19:20

Avec <<1 on a arctan(1/)/2 ?

Pour l'amplitude:

Voulez-vous dire que l'on peut considérer que:

(\alpha\omega_0(z_1 - h_0))^2 \approx 0 ?

Posté par
vanoisere : La bouée qui danse 10-04-20 à 19:34

La première simplification permet de passer au cosinus. Peux-tu évaluer l'erreur relative ainsi commise pour la phase initiale. L'amplitude se simplifie en remarquant  : 2<<1 car comparer une grandeur à zéro n'a pas de sens.  Là aussi, tu peux évaluer l'erreur relative ainsi introduite par cette approximation.

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 19:42

On a donc:

Z(t) =\frac{((z_1-h_0)\omega_0)}{\omega_0}e^{-\alpha\omega_0t}cos(\omega_0t)

Z(t) = (z_1-h_0)e^{-\alpha\omega_0t}cos(\omega_0t)

Est-ce bien cela?

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 19:43

Quant aux évaluations des erreurs relatives, je vous avoue que je n'ai jamais vu ça dans le cours ^^. Donc je ne sais pas vraiment comment faire.

Posté par
vanoisere : La bouée qui danse 10-04-20 à 20:44

Sans la moindre approximation, tu peux déjà commencer par simplifier ton expression de l'amplitude. On obtient :

A=\left(z_{1}-h_{o}\right).\sqrt{1+\alpha^{2}}

L'erreur relative apportée par la simplification déjà évoquée est :

\frac{|A-A_{simplifi\acute{e}}|}{A}=\frac{\sqrt{1+\alpha^{2}}-1}{\sqrt{1+\alpha^{2}}}=0,00183\approx0,18\%

L'approximation me semble acceptable mais je te laisse juge en fonction des exigences de ton professeur.

En revanche : remplacer arctan(1/a) par /2 introduit une erreur relative de 4% ; A toi de juger mais cela me semble un peu juste...

Posté par
Jawad0610re : La bouée qui danse 10-04-20 à 20:50

D'accord, je comprends.

L'approximation de artcan me semble un peu juste aussi.

J'ai donc:

Z(t) = (z_1-h_0)e^{-\alpha\omega_0t}sin(\omega_0t + arctan(\frac{1}{\alpha}))

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !