Inscription / Connexion Nouveau Sujet
Pour la question 10:
Nous n'avons pas vu dans le cours la notion de résonance d'amplitude.
Bien que vous m'ayez dit que, dans ce cas, la fréquence de résonance d'amplitude est proche de la fréquence propre, comment devrions-nous faire pour déterminer cette fréquence de résonance en temps normal avec les informations qui sont à notre disposition? ^^
L'étude en régime sinusoïdal forcé est assez longue et nécessite l'utilisation des nombres complexes. Tu as peut-être étudié un problème analogue : le circuit RLC en régime sinusoïdal forcé. Cette étude n'est à l'évidence pas demandée. Il suffit de répondre que la période de la houle doit être très proche de la période propre.
Le cours sur le sujet a-t-il été étudié ? Si oui, utilise le ; si non, considère le résultat comme un fait expérimental. Les courbes que je t'ai fournies sont le résultat d'une simulation informatique mais elles peuvent aussi être obtenue expérimentalement pour de nombreux oscillateurs soumis à une excitation périodique.
Ma professeure a dit qu'elle fouillerait dans ses archives pour voir si elle a une partie de cours sur ça. Je posterai un message dans le cas où j'ai du nouveau.
Nous n'avons jamais étudié les résonances en cours.
Aussi, mon expression "finale" de Z(t) était-elle correcte? 
J'ai donc:
Tout à fait d'accord. Je me suis amusé à tracer dans le même repère la courbe correspondant à l'équation non simplifiée et la courbe correspondant à l'équation ci-dessus. Impossible de les distinguer, même sur une durée assez longue en choisissant un tracé très fin. En revanche, remplacer l'arctangente par
/2 introduit, au bout de quelques secondes, un écart tout à fait décelable.Ma professeure ne nous as toujours pas transmis de cours sur la notion de résonance. Cependant, voici ce qu'elle m'a écrit:
"il s'agit juste ici de déterminer la période pour laquelle l'amplitude du mouvement (question précédente) est maximale."
Faudrait-il faire une analyse de la fonction obtenue à la question 9?
Si le concepteur du problème attendait une analyse détaillée de Z(t), il le préciserait explicitement dans l'énoncé. On peut ici je pense ce contenter de dire que le mouvement est un mouvement d'oscillation pseudo périodique de pseudo-période sensiblement égale à la période propre avec une amplitude qui décroît exponentiellement avec la constante de temps :
Avez-vous déduit cette relation des expressions que nous avons déterminées précédemment ou est-ce une "formule de cours"?
Faut-il déduire de votre message que la période à laquelle l'amplitude du mouvement est maximale est très proche de la période propre?
Une exponentielle décroissante qui fait intervenir le temps peut toujours s'écrire sous la forme : où
est la constante de temps. Par identification, tu obtiens le résultat que je t'ai fourni. Connaître la constante de temps permet de savoir à "quelle vitesse " décroît l'amplitude. En remarquant : e-5=6,7.10-3
0, on peut considérer que l'immobilité à la position d'équilibre est atteinte au bout d'une durée de 5 environ. Autre façon de présenter les choses : la durée des oscillations amorties est d'environ 5. Durée que tu peux estimer ici...
Je trouve 19,7 s
la période à laquelle l'amplitude du mouvement est maximale serait donc 5*19,798,2s
N'est-ce pas un peu trop élevé?
Bonne question ! Pourquoi ne pas choisir 6 ou 4 ? Il y a effectivement une part d'arbitraire dans ce choix.
e-5 est une valeur un peu inférieure à 1% : cela vaut dire que, pour t=5, les oscillations résiduelles ont une amplitude inférieure à 1% de leur valeurs initiale et très souvent, les instruments de mesures ont une sensibilité telles que, s'ils ont été réglés pour mesurer l'amplitude maximale, ils affichent zéro quand l'amplitude n'est plus que 1% de cette valeur initiale. On peut aussi penser à un enregistreur type oscilloscope qui enregistre Z(t). Pour t>5, la courbe sera confondue avec l'axe horizontal Z=0 compte tenu de l'épaisseur du tracé.
N'est-ce pas un peu trop élevé?
Bien sûr que si ! Relis mon message du 10-04-20 à 18:23.
Je pense que ton professeur a choisi une valeur de C donc une valeur de
aussi faibles pour que des simplifications soient possibles dans l'expressions de Z(t) puis pour obtenir sans calcul la fréquence de résonance. Dans votre message 10-04-20 à 18:23, vous m'indiquez que l'on peut considérer que la fréquence de résonance est très proche de la fréquence propre.
Pour la fréquence propre, on avait:
On vient de déterminer que la période de résonance est 98,2 s. Ce qui donne une fréquence de résonance =
Je suis un peu confus ^^
Je suis un peu confus ^^
Tu mélanges deux notions :
1° : la pseudo période des oscillations, très proche de la période propre : T
To=1,85s : c'est, par exemple, la durée qui sépare deux passages successifs de la bouée en position haute.
2° : la durée 5
qui représente en bonne approximation la durée totale du mouvement avant que la bouée ne retrouve sa position d'équilibre stable. Un rapide calcul montre que, pour cette valeur de aussi petite, la bouée va effectuer environ 53 oscillations avant de s'immobiliser. Totalement irréaliste ! Tu peux faire une expérience toute simple : Tu prends un cylindre en bois. Dans une de ses base tu fixes un morceau de métal de façon qu'à l'équilibre dans l'eau, le cylindre soit à moitié immergé à peu près. Tu appuies sur le cylindre pour l'enfoncer de quelques centimètres par rapport à sa position d'équilibre, tu l'abandonnes à lui-même et tu compte les oscillations avant immobilisation. Cela ne vas surement pas dépasser la dizaine...D'accord je comprends mieux.
Donc pour répondre à la question 10, j'ai juste renseigner cette partie:
1° : la pseudo période des oscillations, très proche de la période propre : T
To=1,85s Avec aussi petit devant 1, la période de résonance est effectivement pratiquement égale à la période propre To.
D'accord, merci beaucoup pour votre aide vanoise.
Je vous souhaite une bonne fin de journée et un confinement en bonne santé
Bonjour,
Voilà ce qu'a posté ma professeure en réponse à ma question concernant la question 10:
"la réponse tient effectivement en une ligne mais il faut vraiment être rigoureux, précisez période propre de quoi? houle? bouée, même chose pour la pseudo période, ce qui vous semble évident ne l'est pas forcément pour le correcteur."
"Le mouvement de la bouée est un mouvement oscillatoire pseudo-périodique de pseudo pulsation très proche de la pulsation propre des oscillations de la bouée. Ainsi, la période de résonance de la bouée est très proche de la période propre de ses oscillations.
La période de houle qui peut faire entrer la bouée en résonance est donc égale à la période propre des oscillations de la bouée."
Est-ce assez rigoureux?
Cette égalité n'est vraie que dans la mesure où les oscillations libres de la bouée sont très peu amorties (<<1). Sinon : tu peux peut-être faire un peu plus concis.
"Dans la mesure où les oscillations libres de la bouée sont très peu amorties (<<1), la période de résonance de la bouée est très proche de la période propre de ses oscillations. Ainsi, la période de houle qui peut faire entrer la bouée en résonance est égale à la période propre des oscillations de la bouée."
Bonjour,
J'ai quelques petites questions.
Pour la question 1:
Nous sommes bien d'accord qu'il faut citer uniquement la poussée d'archimède et le poids et non la force résistive de frottements visqueux car on étudie un système statique?
Pour la question 8:
Lorsque je donne le régime, faut-il que je dise régime pseudo-périodique et sous amorti ou est-ce que régime sous-amorti suffit? Autrement dit, le régime sous amorti implique-t-il un régime pseudo-périodique?
1 : les frottements n'existent que lorsqu'il y a mouvement de la bouée par rapport à l'eau. Il n'existent pas en statique.
8 : en France, les trois cas de mouvement avec frottement visqueux sont qualifiés de :
* pseudo-périodique si <1
* critique si =1
* apériodique si >1
Si ton professeur emploie d'autres termes, tu peux aussi les ajouter. Personnellement, c'est la première fois que j'entends parler de sous amorti à la place de pseudo-périodique...
Merci
Pour l'expression du déplacement Z(t) dans la question 9:
Ne serait-il pas plus simple de passer pas cette expression?
avec
d la pseudo pulsation.
Pour les oscillations libres sans amortissement (=0), la méthode que tu proposes est habituellement plus simple : très souvent, les conditions initiales conduisent à A ou B nul. Pour compris entre zéro et 1 (cas de la question 9), les deux méthodes se valent avec, à mon avis, un léger avantage à celle que tu as précédemment utilisée. Je te conseille de ne rien modifier par rapport à ton travail déjà fait.
Ce qui me chagrinait un peu c'était le fait qu'on a été "obligé" de poser d0 pour simplifier l'équation? Tandis que l'on aurait pas à faire ça avec cette deuxième méthode ^^
on a été "obligé" de poser d0 pour simplifier l'équation? Tandis que l'on aurait pas à faire ça avec cette deuxième méthode ^^
Je ne vois pas le rapport. Il est toujours possible de poser :
A.cos(
.t) + B.sin(.t) = C.cos(.t+
) que la pulsation soit égale à o ou à d...Non Mais c'était plutôt quand on a du déterminer les constantes C et que l'on a dû faire cette approximation.
Je n'ai pas compris ton expression "on a été obligé de poser o pour calculer C et ". Ce calcul aurait aussi pu être fait en posant =d.
Pour la question 9:
D'après le cours, on peut écrire Z(t) sous la forme:
D'après le cours, on a:
Ici on a remplacé
d par 0 pour simplifier l'expression des constantes. Oui parce que 2<<1.
Cette approximation a été justifiée, calcul d'erreur relative à l'appui. Si tu ne veux pas la faire, ne la fais pas .
Pour la rédaction de la question 1, j'ai dit que:
On considère le système incluant la bouée. On est dans un référentiel terrestre supposé galiléen. On choisit un axe vertical Oz orientée vers le bas pour le repère d'étude avec O le centre de masse de la bouée.
Voilà le schéma que j'ai:
Est-ce satisfaisant?
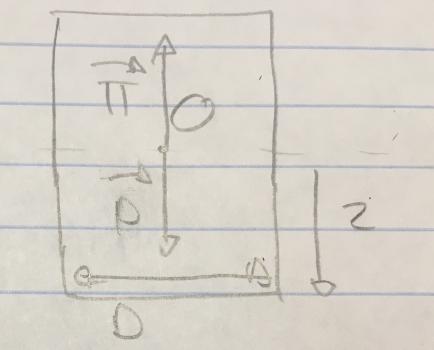
Le système étudié est la bouée ; expression plus précise que "le système inclue la bouée" ; ta phrase suggère que le système n'est pas constitué uniquement de la bouée. O : origine du repère au niveau de la surface libre de l'eau. Centre d'inertie de la bouée : G.
OK pour les vecteurs forces.
Voilà mon schéma pour la question 6 où on a aussi la force exercée par le plongeur.
Vaut-il mieux mettre l'origine du vecteur F en O ou en-dessous de la bouée, là où il y l'attache avec la corde?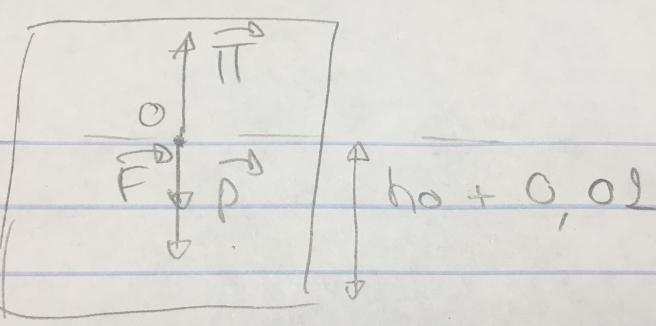 
***Images recadrées (rafraîchir la page)***
Il n'est pas nécessaire de représenter toutes les forces à partir de G. Tu pourrais représenter la force exercée par le plongeur appliquée à la base de la bouée, à la verticale de G.
D'accord merci
Concernant la force résistive de frottement visqueux exercée par l'eau sur la bouée, comment peut-on la représenter sur un schéma? Le vecteur représentant ne change-t-il pas de sens à chaque oscillations?
Bonjour,
Dans ce calcul d'erreur:
Sans la moindre approximation, tu peux déjà commencer par simplifier ton expression de l'amplitude. On obtient :
Ici, on calcul l'erreur associée à la simplication de A. Ne fallait-il pas calculer l'erreur associée à l'approximation
d 0 ?
On avait:
Ne faudrait-il donc pas calculer l'erreur relative suivante?
Les calculs d'erreurs relatives ont déjà été fait pour l'amplitude et la phase initiale. Tu peux aussi le faire pour la pulsation, sachant que tu vas obtenir sensiblement la même chose que pour l'amplitude : 0,18%.
Annuler
connectez vous