Inscription / Connexion Nouveau Sujet
l instant de la colision et le point de collision?
salut
j'ai
 (t)=sin(pi*t)
(t)=sin(pi*t) + 2cos(pi*t)
+ 2cos(pi*t) + 2t
+ 2t
-> -> -> ->
rb(t)=(t-2)i + (t³-3t) j + t²k
j'ai dessiner la trajectoir de ces deux particules avec maple pour 0<=t<=4

désolé énoncé semble mal avoir passé donc je vais le réécrire
j'ai
 a(t)= sin(t*
a(t)= sin(t* )
)  + 2cos(t*
+ 2cos(t* )
)  + 2t
+ 2t 
 b(t)= (t-2)
b(t)= (t-2)  + (t³-3t)
+ (t³-3t)  + t²
+ t² 
j'ai dessiner la trajectoire des particules a et b avec maple
le graph me donne:
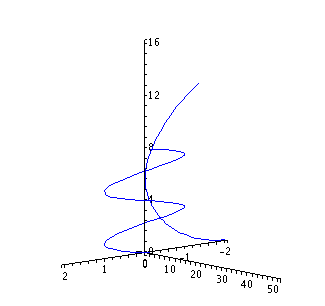
si quelqu'un pouvait me confirmer cela
en même temps, comment on fait avec maple pour avoir l'axe des x, y et z sur le graph?
comment on fait pour montrer que la trajectoire des deux se croisent
est-t'il possible avec maple de déterminer l'instant de la colision et le point de collision? sinon comment on le fait à la main
pour calculer les vecteurs vitesses  a(t) et
a(t) et  a(t) je dois seulement faire la dérivé de:
a(t) je dois seulement faire la dérivé de:
 a(t)= sin(t*
a(t)= sin(t* )
)  + 2cos(t*
+ 2cos(t* )
)  + 2t
+ 2t 
 b(t)= (t-2)
b(t)= (t-2)  + (t³-3t)
+ (t³-3t)  + t²
+ t² 
merci
Les particules entre en collision si on a simutanément les 3 relations:
sin(t.Pi) = t-2
2cos(t.Pi) = t³-3t
2t = t²
2t = t²
t²-2t =0
t(t-2) = 0
--> de cette relation, on voit que t=0 et t=2 sont les seules possibilités.
Mais avec t = 0, les 2 autres relations ne sont pas satisfaites --> t=0 ne convient pas.
Si t = 2
sin(t.Pi) = t-2
sin(2.Pi) =? 2 - 2
0 =? 0 --> la relation sin(t.Pi) = t-2 est satisfaite en t = 2.
2cos(t.Pi) = t³-3t
2cos(2.Pi) =? 2³-3*2
2*(1) =? 8 - 6
2 =? 2 --> la relation 2cos(t.Pi) = t³-3t est satisfaite en t = 2.
t = 2 est le seul instant qui convient.
A ce moment, on a:
Le point de collision a pour coordonnées P(0 ; 2 ; 4)
-----
Sauf distraction et si j'ai bien compris ce qui était demandé. 
l'instant de la colision, le point de collision ainsi que montrer que les trajectoires des deux particules se croisent.... c'est pas équivalent ça?


