Inscription / Connexion Nouveau Sujet
L'équation différentielle -circuit en parallèle
Salut tout le monde, j'espère que vous allez bien, alors je suis en train de préparer au concours et j'ai était vraiment choquée par le HAUT NIVEAU,
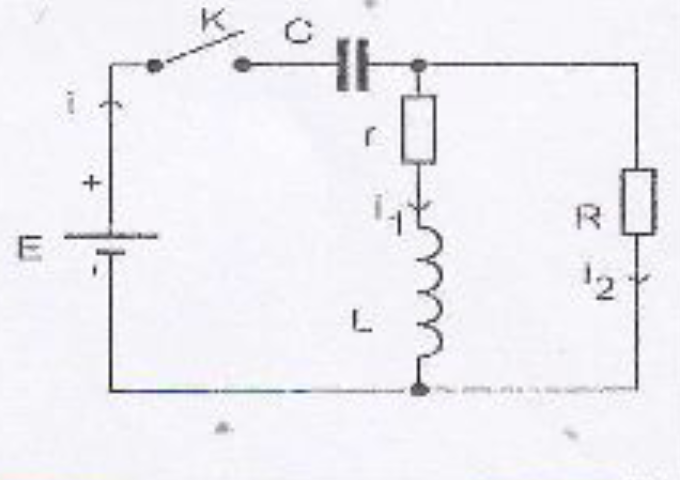
Je me bloque sur une question qui demande de déterminer l'équation différentielle de i2(t)
Je sais que i=i1+i2
Mais je ne sais pas comment déterminer i et i1
*une autre question : est-ce que dans tous les questions où le circuit en parallèle on commence par appliquer la loi des noeuds?
Merciii d'avance
Bonjour
Je ne sais pas ce que tu appelles le haut niveau. Cet exercice est un classique du niveau math sup (Première année CPGE)
La loi des nœuds est effectivement indispensable ici.
Une méthode possible consiste à exprimer chacune des intensités en fonction de la tension u commune à R2 et (L,r) puis à appliquer la loi des nœuds. Sachant que u=R.i2, cela te donnera l'équation différentielle vérifiée par i2.
Merci pour votre réponse!
J'ai été surpris par cette question parce que cette année j'ai eu mon baccalauréat, nous avons étudié seulement des circuits en série, et ça normalement peut paraître un peu difficile pour quelqu'un qui a l'habitude à résoudre toute l'année des circuits en série (mais avec un peu de travail je dois maîtriser ce type d'exercice )
Au fait, c'est une question du même concours ![]() la résistance équivalente
la résistance équivalente
(Cela peut vous montrer combien il est difficile  )
)
C'est un peu plus compliqué que cela et, par rapport au document que je t'ai indiqué, le fait de placer r en série avec L plutôt qu'en dérivation, complique un peu les calculs. Tout de même : je ne suis pas sûr que tu aies pris le temps d'étudier sérieusement ce document... Quelques indications tout de même :
En dérivant par rapport au temps l'expression de la loi des nœuds :
Loi d'Ohm :
Propriété des condensateurs :
Propriété des bobines :
Je te laisse remplacer i et i2 par les expressions en fonction de u obtenues précédemment. En reportant tout cela dans la première expression, on obtient l'équation différentielle vérifiée par u ; facile alors avec la loi d'Ohm d'obtenir celle vérifiée par i2...
Ça me semble correct maintenant; est-ce que vous pouvez poster des liens des cours qui peuvent m'aider à préparer au concours ou bien me donner seulement leurs titres et je serai trèèès reconnaissante !
C'est la bonne équation différentielle. Sinon : tous les ouvrages de prépas (niveau bac+1) pourraient t'aider efficacement.
Et si je veux la solution de cette équation, est-ce que je dois calculer le discriminant comme en mathématiques et suivre les mêmes étapes ?
oui ; cela est expliqué très en détail sur le document que je t'ai fourni avec les trois types de solutions...


