Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Introduction à la mécanique des fluides

Posté par
Kovak 05-03-20 à 14:52

Bonjour,

Je souhaiterais résoudre un exercice d'introduction à la mécanique des fluides, seulement je ne suis pas sûr de mes réponses..

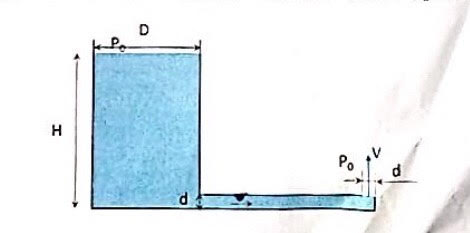
Voici l'énoncé (voir photo pour le schéma) :
Sur un jet d'eau alimenté par un réservoir, une conduite horizontale de diamètre d amène l'eau à la vitesse v du réservoir d'eau. Le trou par lequel s'échappe l'eau du jet a un diamètre d. Dans toute la suite on considérera que la vitesse V de l'eau au passage par ce trou est constante. Les dimensions du réservoir sont très grandes devant D et d de sorte que l'altitude H à laquelle se trouve la surface libre de l'eau dans le réservoir sera considérée comme constante. La pression qui règne au sommet du réservoir est à la pression atmosphérique p_{0}.
Données : H=30cm, D=20cm, d=3nn, v=10m/s, g=10m/s

1) Écrire la conservation du débit volumique d'eau Qv entre la conduite horizontale et le jet. Sachant quel D>>d, quelle conséquence ceci a-t-il sur les vitesses  v et V ?

2) Avec l'équation de Bernoulli, exprimer la pression  p dans la conduite horizontale pour que l'eau soit expulsée à la vitesse V. Calculer  p-p_{0}.

3) À quelle altitude h s'élève le jet d'eau ? On négligera l'effet de la résistance de l'air sur le jet. Calculer numériquement h.

(viscosité de l'eau à température ambiante : \eta =10^{-3} Pa s)
4) On prend maintenant en compte les forces de viscosité dans la conduite horizontale. Calculer le nombre de Reynolds dans la conduite horizontale, en déduire la nature de l'écoulement.

5) Dessiner le profil de vitesse de l'eau dans une section de la conduite. Expliquer qualitativement la forme du profil ? Comment s'appelle ce type d'écoulement ?

Mes réponses :
1) Débit volumique : Q_{v}=\frac{\Delta V}{\Delta t}=Sv
Donc Q_{v}=\pi (\frac{d}{2})^{2}v=\frac{\pi }{4}d^{2}v
Le débit volumique est conservé car les vitesses v et V sont les mêmes et restent constantes car la diamètre de la conduite horizontale est égal à celui du trou.

2) Avec l'équation de Bernoulli j'obtiens (z_{c} et z_{t} altitude de la conduite et du trou):
\frac{1}{2}\rho v^{2}+P+\rho gz=constante
\Rightarrow \frac{1}{2}\rho v^{2}+P+\rho gz_{c}=\frac{1}{2}\rho V^{2}+P_{0}+\rho gz_{t}
\Leftrightarrow P=\frac{1}{2}\rho (V^{2}-v^{2})+P_{0}+\rho g(z_{t}-z_{c})
\Leftrightarrow P=\frac{1}{2}\rho (V^{2}-v^{2})+P_{0}  car la conduite et le trou sont à la même hauteur donc z_{t}-z_{c}=0.

Donc P-P_{0}=\frac{1}{2}\rho (V^{2}-v^{2})

3) Toujours avec Bernoulli,  \frac{1}{2}\rho (v^{2})+P+\rho g(z_{c})=\frac{1}{2}\rho (V^{2})+P_{0}+\rho g(z_{t})
\Leftrightarrow \frac{1}{2}\rho (v^{2}-V^{2})+P-P_{0}=\rho g(z_{t}-z_{c})
\Leftrightarrow \frac{1}{2}\rho (v^{2}-V^{2})+P-P_{0}=\rho gh
\Leftrightarrow h=\frac{1}{\rho g}(\frac{1}{2}\rho (v^{2}-V^{2})+P-P_{0}))

À partir de là je bloque, est-ce que P-P_{0} doit être nul car les deux pressions sont égales ? Comment calculer numériquement h sans avoir la valeur numérique de V ? Quel est l'intérêt de dire que l'altitude H du réservoir est constance, qu'est-ce que ça peut changer dans mes calculs ? Je ne sais pas si mon raisonnement depuis le début est bon ou pas, merci d'avance pour votre aide.

Introduction à la mécanique des fluides

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 17:21

Bonjour
Pour 1, la conservation du débit conduit simplement à :
D2.V=d2.v
Donc si D>>d , V par rapport à v ?
Pour 2 et 3 : il est possible d'appliquer le théorème de Bernouilli entre l'entrée dans le tuyau horizontal et la sortie.
Il est aussi possible d'appliquer le théorème de Bernouilli entre la surface libre à l'altitude H et l'orifice de sortie à l'altitude nulle.

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 18:01

Pour la question 1) on cherche la conservation du débit volumique entre la conduite horizontale et le jet et non le réservoir, je n'ai pas compris pourquoi nous devons inclure la dimension du réservoir D dans l'équation de conservation ? Du coup si D>>d on a v>>V ?

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 18:46

Je me suis "emmêlé" les pinceaux dans les notations.
Je reprends  (toutes mes excuses...) :
Appelons V_1=-\frac{dH}{dt} la vitesse de descente du niveau d'eau dans le bassin. La conservation du débit  conduit à :
D2.V1=d2.v
Supposer D>>d  conduit à V1<<v ; ce qui conduit à négliger la vitesse de descente du niveau d'eau dans le bassin et donc à considérer H comme une constante.
Ensuite, si tu appliques le théorème de Bernoulli à la surface libre, à l'entrée dans le tuyau et à la sortie (trou), tu obtiens :
P_{o}+\rho.g.H+\frac{1}{2}\rho.V_{1}^{2}=P+\frac{1}{2}\rho.v^{2}=P_{o}+\frac{1}{2}\rho.V^{2}

avec v=V , P=Po et le terme en V12 négligeable.

Pour être sûr de bien pouvoir négliger le terme en V12, peux-tu fournir la valeur de d : ton énoncé paraît bizarre à ce sujet ?[/tex]

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 20:32

Merci pour votre réponse. Oui mes excuses j'ai fais une faute de frappe dans l'énoncé, ce n'est pas "d=3nn" mais d=3mm.

D'accord donc si je poursuis le développement de l'équation de Bernoulli, on obtient :
P+\frac{1}{2}\rho v^{2}=P_{0}+\frac{1}{2}\rho V^{2}
\Leftrightarrow P=P_{0}  car v=V
donc P-P_{0}=0.

Pour la question 3, est-ce que mon équation de Bernoulli est bonne ?
Parce que si je la refais (en prenant en compte que v=V et P-P_{0}=0) et que j'isole h j'ai :
P+\frac{1}{2}\rho v^{2}=\frac{1}{2}\rho V^{2}+P_{0}+\rho gh
\Leftrightarrow \frac{1}{2}\rho (v^{2}-V^{2})=\rho gh
\Leftrightarrow \frac{1}{2g}(v^{2}-V^{2})=h
\Leftrightarrow h=0

Ce qui donne un jet de 0m de hauteur...

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 20:54

En tenant compte aussi de la conservation du débit  :
V=v  et P= Po
La double égalité que j'ai écrite  conduit à  :
v2 =V2 = 2.g.H

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 21:04

Je ne vois pas comment trouver l'altitude h du jet avec ce qu'on obtient de la double égalité de la question 2 : 2gH=v^{2}=V^{2}. Car ici on a seulement la hauteur H de l'eau dans le réservoir qui est présente dans l'égalité mais H \neq h il me semble

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 21:15

Une fois obtenue la vitesse de sortie V de l'eau, tu appliques à une goutte la relation fondamentale de la dynamique en négligeant les frottements ou, si tu préfères, le théorème de l'énergie cinétique. Tu vas obtenir  :
V2 = 2g.h
Cela donne bien : h = H  mais bien sûr la réalité est plus compliquée à cause des frottements de l'air  et de la viscosité de l'eau.

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 21:58

Merci c'est bien plus clair pour moi après le théorème de l'énergie cinétique.

Pour la suite, la question 4 j'ai donc calculé le nombre de Reynolds R_{e} :
R_{e}=\frac{vd}{\eta }=\frac{10*3*10^{-3}}{10^{-3}}=30
R_{e}>1 Il s'agit donc d'un écoulement inertiel où la viscosité est très faible. Est-ce correct ?

J'ai cependant pas trop compris la dernière question (5), je ne sais pas ce qu'est un profil de vitesse.. Puisque la vitesse reste constante le long de la conduite horizontale de diamètre d constant, le profil est celui d'une vitesse v constante ?

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 22:24

Attention  : ne pas confondre viscosité dynamique et viscosité cinématique.  Revois ton calcul du nombre de Reynolds.  La fin de l'exercice relève simplement du cours.

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 22:43

Ah, donc je doit plutôt utiliser cette expression du nombre de Reynolds : R_{e}=\frac{\rho vd}{\eta }
\Rightarrow R_{e}=\frac{1000*10*3*10^{-3}}{10^{-3}}=3000 C'est bien cela ?

Posté par
vanoisere : Introduction à la mécanique des fluides 05-03-20 à 23:00

Étourderie de calcul : Re=30000.

Posté par
Kovakre : Introduction à la mécanique des fluides 05-03-20 à 23:02

Oui 30000 pardon.. merci beaucoup d'avoir pris le temps de m'aider !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !