Inscription / Connexion Nouveau Sujet
Interférences lumineuses
Bonjour ,
Svp j'ai du mal à écrire l'expressions complexe des vecteurs champs électromagnétiques . J'aurais besoin de ça pour pouvoir déterminer l'expression de l'intensité lumineuse I en un point M de l'écran ( Fentes de Young ) . Merci
Bonjour
En optique physique, on utilise une représentation scalaire du vecteur champ et les conventions sont celle utilisées en électricité en régime sinusoïdal
Bonjour
En optique physique, on utilise une représentation scalaire du vecteur champ et les conventions sont celle utilisées en électricité en régime sinusoïdal
Ce que tu indiques correspond au vecteur champ électrique associée à une onde plane monochromatique polarisée rectilignement se propageant suivant la direction et le sens du vecteur k avec .
Dans le cadre de l'optique ondulatoire, les conditions expérimentales sont toujours telles que les vecteurs champs qui se superposent sont pratiquement colinéaires. On peut ainsi remplacer une somme de vecteurs champ par une somme de valeurs algébrique. A une onde n°1 se propageant à partir d'une source quasi ponctuelle S1, on associe le signal algébrique :
auquel on peut associer le complexe :
A une onde n° 2 se propageant à partir d'une source S2 de même fréquence et en phase avec S1, on associe le signal :
avec
Il faut alors additionner les deux signaux puis
écrire que l'intensité lumineuse est proportionnelle au carré de l'amplitude soit proportionnelle au produit de la somme complexe par son conjugué :
Il te faut trouver un cours structuré sur ce sujet. Voici un document qui pourra t'aider mais son niveau dépasse peut-être les exigences de ton programme. N'hésite pas à poser des questions sur les points précis que tu ne comprends pas.
![]()
Bonjour à vous deux,
@mrlne : pourrais-tu utiliser au maximum les possibilités offertes par le site pour les formules en lieu et place de photos de manuscrits :
Bonjour à vous deux,
@mrlne : pourrais-tu utiliser au maximum les possibilités offertes par le site pour les formules en lieu et place de photos de manuscrits :
[faq]symboles[/faq]
Je le ferai désormais . Je veux dire 
Ce que tu indiques correspond au vecteur champ électrique associée à une onde plane monochromatique polarisée rectilignement se propageant suivant la direction et le sens du vecteur k avec
Dans le cadre de l'optique ondulatoire, les conditions expérimentales sont toujours telles que les vecteurs champs qui se superposent sont pratiquement colinéaires. On peut ainsi remplacer une somme de vecteurs champ par une somme de valeurs algébrique. A une onde n°1 se propageant à partir d'une source quasi ponctuelle S1, on associe le signal algébrique :
auquel on peut associer le complexe :
A une onde n° 2 se propageant à partir d'une source S2 de même fréquence et en phase avec S1, on associe le signal :
Il faut alors additionner les deux signaux puis
écrire que l'intensité lumineuse est proportionnelle au carré de l'amplitude soit proportionnelle au produit de la somme complexe par son conjugué :
Il te faut trouver un cours structuré sur ce sujet. Voici un document qui pourra t'aider mais son niveau dépasse peut-être les exigences de ton programme. N'hésite pas à poser des questions sur les points précis que tu ne comprends pas.
La constante de proportionnalité que j'ai appelée k dépend de la définition donnée à l'amplitude... Elle peut valoir 1/2 dans certaines conditions mais l'essentiel n'est pas là : as-tu bien compris la démonstration ? Es-tu capable de l'appliquer à un dispositif interférentiel simple ?
Il faut être capable de déterminer la différence de marche d2-d1 en fonction de la distance "a" entre les deux sources, de la distance D des sources au plan d'intervention et de l'abscisse x d'un point sur l'écran...
Concernant la différence de marche d2-d1 pour un dispositif interferentiel simple . J'ai compris comment exprimé cette différence de marche là .
Mon soucis maintenant c'est de connaître quand vous dîtes "dans certains" pourquoi particulièrement dans notre cours ça vaut 1/2 ? Si je peux vous poser cette question .
L'intensité lumineuse (en toute rigueur, il serait préférable de parler d'éclairement...) fait intervenir la valeur moyenne du carré du vecteur champ électrique, donc la valeur moyenne du carré d'une fonction sinusoïdale du temps. Or, la valeur moyenne, calculée sur une période, de est \frac{1}{2}A^{2}. C'est probablement à cause de cela que ton cours introduit ce coefficient 1/2 mais cela ne règle pas tous les problèmes : le carré de l'amplitude d'un vecteur champ électrique n'a pas la même dimension physique qu'une intensité lumineuse. Il y a donc bien une constante de proportionnalité qui intervient pour obtenir l'intensité lumineuse. Bref : tout cela n'est pas très important : ce qui importe dans les problèmes, c'est le rapport I/Imax où Imax représente l'intensité maximale observable en certains points de l'écran.
Maintenant vous avez dit en toute rigueur qu'il serait mieux de parler d'éclairement . J'aimerais connaître pourquoi . Merci
En toute rigueur, l'éclairement représente la puissance moyenne reçue par unité de surface de l'écran :
et se mesure en W/m2
On démontre en électromagnétisme :
L'éclairement est bien proportionnel au carré de l'amplitude du champ électrique ; on retrouve le coefficient 1/2 de ton cours mais pas seulement... C'est pour cela que j'ai préféré utiliser une constante k avec .
Pour des raisons essentiellement historiques, dans d'autres domaines où interviennent des ondes, l'acoustique en particulier, on appelle intensité la puissance moyenne par unité de surface. La tendance actuelle des programmes est d'harmoniser la situation et d'appeler indifféremment éclairement ou intensité la puissance moyenne par unité de surface.
En optique, l'intensité est, en toute rigueur la puissance par unité d'angle solide :
Tu n'as sans doute jamais entendu parler d'angle solide. Pas grave : il suffit d'admettre que, dans les conditions habituelles d'études des interférences, intensité lumineuse et éclairement sont deux grandeurs proportionnelles...
Tout cela est bien compliqué...
En pratique : garde les habitudes de ton professeur et retient l'essentiel : l'intensité lumineuse comme l'éclairement sont deux grandeurs proportionnelles au carré de l'amplitude du signal complexe résultant de la superposition des ondes. Peu importe la constante de proportionnalité.
Ok merci . J'ai compris
Et justement concernant les deux premières formules que vous avez données . J'ai eu à déterminer l'intensité d'une onde sinusoïdale j'ai trouvé I=1/2 × ×c(Aw)² .
×c(Aw)² .
Mon problème est de savoir si le milieu de propagation de l'onde est supposé l'air . Dans la formule de I là la seule grandeur qui dépend du milieu de propagation est  car le reste comme c=vitesse de phase , A= amplitude , w= pulsation dépendent de l'onde . Donc pour les calculs au cas où le milieu de propagation est l'air je remplace tout simplement
car le reste comme c=vitesse de phase , A= amplitude , w= pulsation dépendent de l'onde . Donc pour les calculs au cas où le milieu de propagation est l'air je remplace tout simplement  par
par  air . Cela est correct ?
air . Cela est correct ?
En passant je donne l'équation de propagation de l'onde
y= 2×10-3sin(18x-600t+30°) ( En mètres ) .
Merci
De quelle type d'onde s'agit-il ? Onde transversale le long d'une corde peut-être... S'il s'agit bien de cela, le milieu de propagation est la corde...
Attention : une phase se mesure habituellement en radians...
S'il s'agit d'une onde transversale le long d'une corde, on ne peut pas définir une puissance moyenne par unité de surface.
Tu peux poster l'énoncé intégral de l'exercice ?
Ton message de 14h50 est incohérent. Je ne peux pas t'aider plus sans un énoncé intégral de l'exercice et éventuellement un scan du schéma s'il est fourni.
Voici l'énoncé de l'exercice
Exercice :
L'équation de propagation d'une onde sinusoidale transversale est donnée par :
y=2 10-3Sin(18x-600t+
10-3Sin(18x-600t+ /3) m
/3) m
1) Déterminer l'expression de l'intensité de cette onde .
2) Application numérique : le milieu de propagation est supposé l'air . Trouver la valeur de cette intensité .
Mes réponses
1) je trouve I=
 c(Aw)2
c(Aw)2
où A= amplitude , w= pulsation , c=vitesse de phase= ,
 =masse volumique
=masse volumique
2) Si le milieu supposé est l'air alors alors I=
 airc(Aw)2 car seule
airc(Aw)2 car seule  dépend du milieu du propagation .
dépend du milieu du propagation .
Les ondes se propageant dans l'air, en dehors des ondes électromagnétiques sont les ondes acoustiques. Ces ondes sonores sont longitudinales et non transversales. Leurs amplitudes ne sont pas de l'ordre du millimètre et leurs vitesses de phase ne sont pas de l'ordre de (600/18)m/s.
Je t'ai donné mon point de vue : cet énoncé est incohérent pour les nombreuses raisons expliquées précédemment...

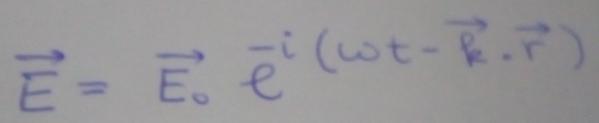

 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum

