Bonjour,
Pourriez vous m'expliquer un point de calcul que je n'ai pas compris

Une goutte liquide, incompressible, de forme cylindrique se trouve entre 2 plans parallèle.
Le champ des vitesses à l'intérieur de la goutte est à symétrie cylindrique v(M,t)= vr(r,y,t) ur + vy(y,t)uy
A partir d'un bilan de matière sur le cylindre de fluide de rayon r, de hauteur dy montrer que vr= (r/2) d(vy)/dy (dérivée partielle)

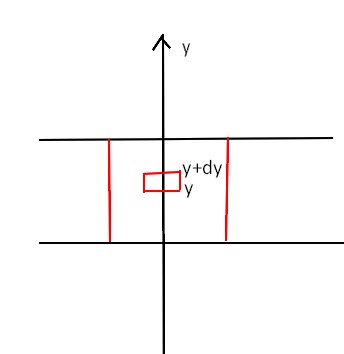
=>Le fluide étant incompressible le débit volumique à travers une surface fermée est nulle. On prend donc comme volume de contrôle le cylindre de rayon r compris entre y et y+dy


J'ai un problème quant au 2eme terme. Mon "y'" signifie bien qu'on prend un M de la surface latérale et qu'on intégre ensuite sur toute la surface latérale donc y' varie avec dS_lat = dy' * 2 Pi r donc on ne peut pas sortir impudemment le vr (r,y',t) de l'intégrale.. et pourtant le résultat indique le contraire.
Explications svp?