Inscription / Connexion Nouveau Sujet
Insertion d'un atome dans un alliage
Bonjour,
J'ai un contrôle que je dois rendre ce soir je l'ai presque terminé mais il y a juste la derniere question que j'ai du mal à comprendre.
Au départ on a du Cu qui cristallise en cfc. Ensuite il y a une liste d'atomes donnés et on me demande ceux qui peuvent s'insérer dans la maille du Cu. J'ai répondu à la question par la formule de la condition d'insertion. La dernière partie le cuivre forme avec le berylium un alliage en cfc, et on demande quels atomes de la liste précédente peuvent s'insérer dans l'alliage. J'arrive pas à répondre à cette question existe-t-il une formule pour démontrer l'insertion d'un atome dans un alliage.
Merci à l'avance.
Bonjour
Il te faut calculer l'habitabilité des sites et la comparer aux rayons atomiques fournis. C'est la même méthode que dans ton premier cas. Si tu veux plus de détail, fournis les renseignements qui te sont donnés par l'énoncé concernant l'alliage fer béryllium.
S'il y a un schéma, tu peux le scanner et le poster ici.
Bonjour j'ai calculé le rayon max quand il s'agissait de la maille de cuivre par la formule 2(Rcu+Rmax)=a.
Pour l'alliage cuivre béryllium on a le Rbe=112pm et Rcu=135pm
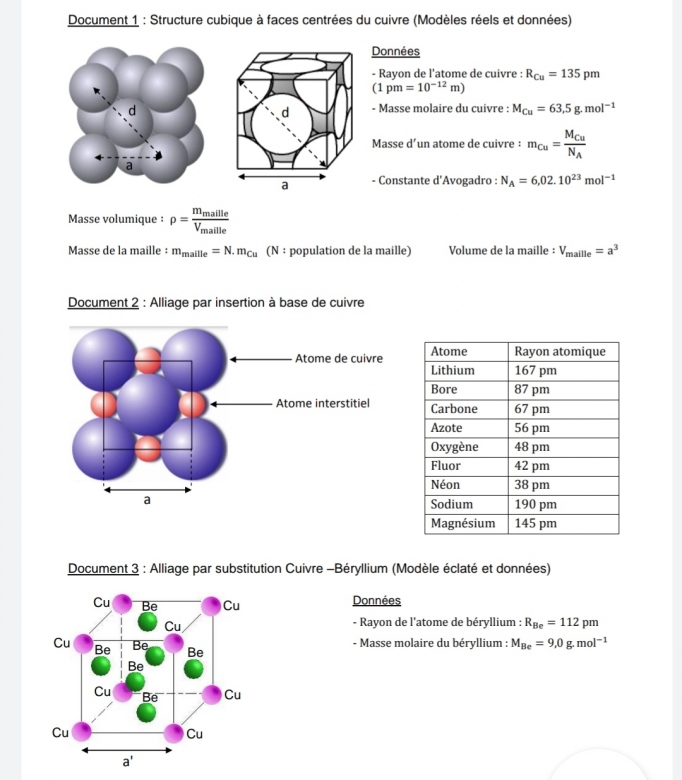
En fait je veux savoir si pour trouver la condition d'insertion d'un atome dans un alliage c'est la même formule que j'ai appliqué pour le cas précédent
Tu as besoin de déterminer les habitabilités des sites octaédriques et des sites tétraédriques. La notion de site interstitiel : cela te parle ? C'était déjà la méthode à utiliser dans le premier cas. Tu parles d'une "formule"... Il serait peut-être préférable de comprendre ce qui se passe plutôt que d'appliquer une formule...
Cela dit : la méthode est bien la même puisque l'alliage Ce-Be est un alliage par substitution et que les rayons atomique de Cu et Be sont très proches.
Du coup tous les atomes qui se sont insérer dans la structure à base de cuivre s'insereront également dans la structure de l'alliage Cu-Be ? Puisque les rayons atomiques du cuivre et du béryllium n'ont pas énormément de différences.
N'ayant aucun renseignement sur les éventuelles déformations de la maille dues à la petite différence entre les rayons de Cu et Be, je ne crois pas que tu puisses en dire plus.
Avec un énoncé complet, je vais pouvoir t'aider plus efficacement (du moins j'espère !  )
)
Mon message précédent de 15h25 est à reprendre : l'énoncé fournit bel et bien dans sa partie C l'influence du béryllium sur la maille : celle-ci est devenue un peu plus petite tout en restant de type cfc.
Tu peux donc reprendre ta formule donnant Rmax à condition de remplacer le paramètre "a" de la maille par a'.
J'y ai déjà pensé à calculer Rmax en utilisant a' la formule étant 2(R...+Rmax)=a' et le R... sera le rayon du cuivre ou du béryllium ?
Bonne question... Pour être cohérent, il faut calculer le rayon R' d'atomes tous identiques correspondant à une maille cfc de paramètre a'. Tu vas remarquer que cela conduit sensiblement à la moyenne des deux rayons atomiques.
Donc il faudra que je calcule R'=(Rcu+Rbe)/2 ? Ça semble quand même étrange comme raisonnement. Sinon je viens de penser à autre chose on est d'accord que l'atome ne pourra s'insérer que soit sur l'espace au milieu des sommets qui sont constitués de Cu soit sur l'espace qu'il ya a quand on considère que l'atome de Be. Étant donné que j'ai calculé Rmax en considérant Rcu, il ne serait pas judicieux de calculer R'max qu'avec Rbe et de donner une conclusion par rapport aux deux valeurs de Rmax ?
Je sais pas si c'est bien expliqué 😅
Puisque l'énoncé de mande d'assimiler la maille à une maille cfc de paramètre a', je pense qu'il faut déterminer R' comme le rayon d'atomes tous identiques qui conduirait à une telle maille. Puisque les atomes sont en contact le long d'une diagonale de face :
Cela conduit très logiquement à une valeur comprise entre les deux rayons atomiques et proche de leur valeur moyenne.
Dans ce cas R'=2Rcu+2Rbe puisque les atomes sont en contacts sur la diagonale. C'est plutôt 2Rcu+Rbe=a'sqrt(2)
Je viens de lire l'énoncé en entier... Je n'avais pas vu auparavant que les substitutions s'opéraient obligatoirement au centre de chaque face. Il ne faut donc pas, comme je l'envisageait précédemment, raisonner sur des valeurs moyennes.
Dans de telles conditions, tu as bien comme tu l'as écris.
Considère maintenant un atome interstitiel sphérique qui occupe un site octaédrique : centre de la maille cubique ou milieu d'une arête. Le rayon maximum de cet atome correspondra à la mise en contact de cet atome avec les plus gros des atomes de la maille, donc avec les atomes de cuivre.
Tu as donc : a'=2RCu+2Rmax
Si, indirectement, car il faut commencer par comprendre les conséquences de l'inégalité : RBe<RCu sur l'habitabilité du site octaédrique.
Bon bah je vais garder la formule a'=2RCu+2Rmax pour trouver Rmax même si je suis dubitatif du fait qu'il n'y ait pas le Rbe dans la formule pour trouver Rmax.
Tu trouves bizarre que RBe n'intervienne pas. Il intervient deux fois en fait.
Une fois comme expliqué dans mon message de 17h57 ;
Une fois dans l'expression de Rmax :
Tu écris : a'=2RCu+2Rmax ; OK mais il ne faut pas oublié que dans la partie C, a' a été calculé par la formule rappelée à 18h44. Une synthèse de cela conduit à :
Je te laisse simplifier. Il s'agissait juste pour moi de te faire remarquer que RBe intervient dans le résultat.



