Bonjour. Voici un exercice tiré d'un examen concours. Je vais vous soumettre mes idées de solution :

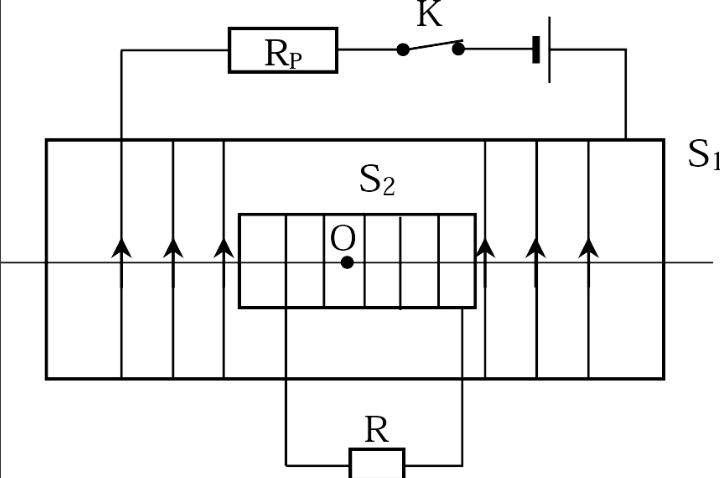
Un solénoïde  S1,  de  centre  O, de  longueur  L  =  0,8  m,  comporte  n1  =1000  spires  par  mètre  de longueur.   Ses  bornes  sont  reliées  à  un  générateur  par  l'intermédiaire  d'un  interrupteur  K. Lorsqu'on  ferme  K,  S1  est  traversé  par  un  courant  continu  et  constant  I=5  A,  dont  le  sens  est indiqué  sur  le  schéma  ci-dessous.
1.  Représenter  au  point  O, le  vecteur  B1 créé  dans  S1.

2.  Calculer  la  valeur  B1.

3.  Un autre solénoïde  S2,  de  petites  dimensions  par  rapport  à  celles  de  S1  est  disposé  à l'intérieur  de  S1. S1  et  S2  sont  coaxiaux  et  orientés  dans  le  même  sens.   Le  solénoïde  S2 comporte  N2=  500  spires  de  surface  s  =  3  cm2. Un  conducteur  ohmique de  résistance  R=  10  Ω  est  branché  aux  bornes  de  S2.

3.1.  Expliquer  pourquoi  il  apparait  dans  S2  un  courant  électrique  quand  on  ferme  ou on ouvre  le  circuit  de  S1.

3.2  Justifier  le  sens  du  courant  (ascendant  ou  descendant) dans  S2  à  la  fermeture  du circuit  de  S1.

   4.1.  Donner  l'expression  de  la  valeur  du  flux  ɸ2  dans  S2  en  fonction  de  N2,  B1 et  s.

4.2.  Calculer  la  valeur  de  ɸ2.

4.3.  Calculer  la  valeur  de  la  quantité  d'électricité  Q  qui  a  traversé  S2  à  l'ouverture  de  K. 5.

Le  solénoïde  S1,  est  maintenant  alimenté  par  un  générateur  de  courant  alternatif sinusoïdal  d'expression  i1=  5 cos314t.

5.1  Établir  l'expression  de  la  force  électromotrice  d'induction  e  dans  S2.  

5.2.  En  déduire  l'expression  de  l'intensité  du  courant  i2  qui  traverse  S2. On négligera  la  tension  aux  bornes  de  S2  devant  celle  du  conducteur  ohmique  de résistance  R.