Inscription / Connexion Nouveau Sujet
Induction électromagnétique dans un circuit
Bonjour,
J'ai un peu de mal à répondre aux questions d'un exercice portant sur l'induction dans un circuit carré. J'ai essayé de tout détaillé, mon énoncé ainsi que mes réponses.
Voici l'énoncé :
Un circuit métallique de forme carré de côté a et de résistance R, repose à plat sur une table. Un fil rectiligne parcourut par un courant I passe juste au-dessus du circuit et parallèlement à un des côtés. On considèrera que le fil se trouve dans le plan du circuit, sans contact ohmique entre les deux.
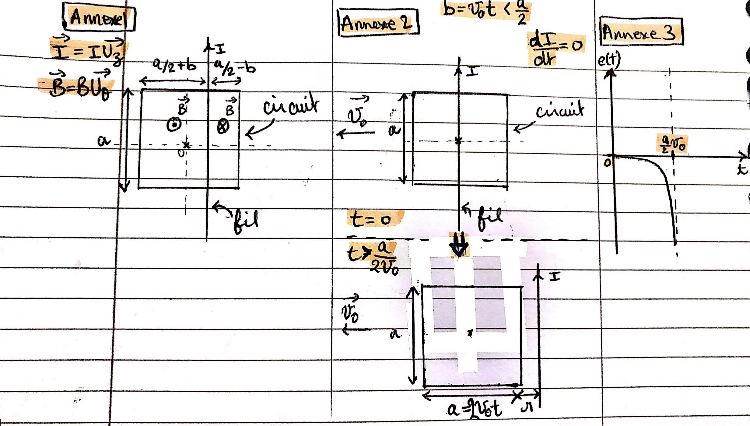
1) Le fil ne passe pas par le centre du circuit, on augmente le courant circulant dans le fil (dI/dt>0). Déterminer la force électromotrice induite dans le circuit. Déterminer ensuite le sens de l'intensité du courant qui circule dans le circuit. (voir image jointe annexe 1)
2) Le courant I est maintenu constant, . Le centre du circuit se trouve sur le fil à t=0 et on déplace le circuit perpendiculairement au fil avec une vitesse constante
. Déterminez le sens et l'intensité du courant qui apparait dans le circuit. (voir image jointe annexe 2)
Voici mes réponses :
1) Le fil est décalé d'une distance b par rapport au centre, avec b<a/2. On utilisera ici les coordonnées cylindrique avec le courant et le champ magnétique
On calcul le flux "des deux cotés" du fil car le vecteur champ magnétique n'est pas constant, il tourne autour du fil.
On en déduit la force électromotrice :
Sens et intensité du courant I :
Donc si dI/dt>0, i<0, ce qui veut dire que i sera vers le bas () et d'après la règle de la main droite,
sera selon
.
D'après le formule de la loi de Lenz-Faraday, le flux magnétique augmente si I augmente.
2) Le circuit se déplace ici vers la gauche à une vitesse constante avec un courant constant
.
est la distance qu'il faut parcourir pour avoir le circuit dans son entièreté à gauche du fil. Donc si on reprend le raisonnement de la question précédente on a pour le flux :
Donc la force électromotrice e vaut :
Quand le circuit ne s'est pas encore déplacé dans sa totalité vers la gauche du fil (donc quand ) on a e<0 soit
.
Si , le flux augmente et créé un flux magnétique induit qui sera négatif afin de s'opposer à l'augmentation du flux magnétique. C'est le principe de la loi de Lenz.
Là où je bloque est sur l'intégration du flux quand le circuit est passé de l'autre coté dans son entièreté, donc quand .
Je pose la longueur r, la distance entre le coté droit du circuit et le fil lorsque le circuit est passé de l'autre côté.
Donc pour la force électromagnétique e on a :
Mais à partir de là je ne sais plus trop si c'est correct. Je ne sais donc pas si la loi de Lenz est là aussi vérifiée, et je ne sais pas non plus comment continuer mon graph e(t) (voir image jointe annexe 3)
J'espère avoir pu me faire comprendre, et merci d'avance pour le temps que vous m'accorderez.
Bonjour,
Pour le 1, le principe est correct, mais il est difficile de conclure pour les signes en absence d'indication (même si on peut deviner). Règle de base des calculs d'induction : orienter les circuits.
"D'après la loi de Lenz-Faraday, le flux magnétique augmente si I augmente." Vous voulez parler du flux de B induit ?.
D'autre part diverge, il vaut mieux sommer uniquement sur l'aire qui ne se compense pas entre droite et gauche , soit entre (a/2+b) et (a/2-b) à gauche. Pour éviter la divergence, il faut prendre le fil de rayon fini (la somme uniquement à gauche cache le problème que l'on retrouve lorsque a=2b)
Pour le 2, début OK pour le principe
"Quand on a e<0 soit I_{0}<0." C'est plutôt l'inverse
est une donnée et le signe de e s'en déduit.
"quand le circuit est passé de l'autre coté", il y aura eu des problèmes avant, e va diverger pour .
Une fois "passé de l'autre côté", l'un des bords est à et l'autre à
(votre r). Avec vos notations le côté gauche est à r+a et r=r(t) !
Au vu des problèmes posés par le passage du fil au dessus d'un bord, il se peut que l'exercice suppose que cela n'arrive pas.
D'accord merci pour votre réponse.
Donc quand le circuit passe entièrement de l'autre coté, pour calculer le flux je dois donc intégrer B.dS de cette manière ?
Comment je peux montrer que la fem. diverge quand ? Est-ce parce que les bornes de l'intégrales pour calculer le flux s'écrivent de cette manière
? Et qu'est-ce que cela signifie physiquement parlant, je n'arrive pas trop à saisir pourquoi la fem. diverge à cet endroit..
quand le circuit passe entièrement de l'autre coté, je dois donc intégrer B.dS de cette manière ?
C'est bien cela.
Comment je peux montrer que la fem. diverge quand a=2v_{0}t ?
Vous écrivez
Et il en effet clair que
Qu'est-ce que cela signifie physiquement parlant ?
Pas grand chose, sinon que le modèle du fil infiniment fin collé sur le cadre conduit à un champ B infini quand
J'obtiens donc pour le flux
et pour la fem .
Donc pour conclure, si , alors
. Sachant que
, on en déduit que
. Donc le flux
diminue à mesure que le circuit s'éloigne du fil. Le flux magnétique induit
est lui positif et s'oppose ainsi à la diminution du flux magnétique
. Ce qui vérifie la loi de Lenz.
Quand on regarde le schéma, à gauche du fil, pointe vers l'écran, soit en opposition au champ magnétique initial.
Est-ce bon ?


