Inscription / Connexion Nouveau Sujet
Indice de réfraction
Bonjour,
Un prisme a une section droite ABC telle que A=90° ; B= 60°.
Un rayon incident arrive en I1 sur la face AB sous un angle d'incidence i1 = 45°.
a) Déterminer la valeur n de l'indice de réfraction du prisme à partir de laquelle il y a réflexion totale du rayon I1I2 sur la face BC.
b) Déterminer la valeur n0 de l'indice de réfraction que devrait avoir ce prisme pour que l'angle r1 en I1, soit égal à i2 en I2 sur la surface BC. On a toujours i1= 45°
Je bloque sur la première question.
Bonsoir
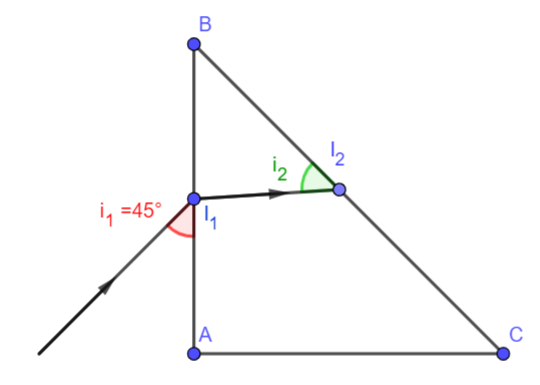
Il faut commencer par faire une figure propre et y tracer un rayon dans le plan principal du prisme. Tu peux scanner le schéma et le poster ici. Plus facile de t'aider ainsi.
A toi alors d'en imaginer un à partir des indications fournies par l'énoncé.Je te laisse réfléchir et poster un schéma ; je t'aiderai à le compléter si nécessaire...
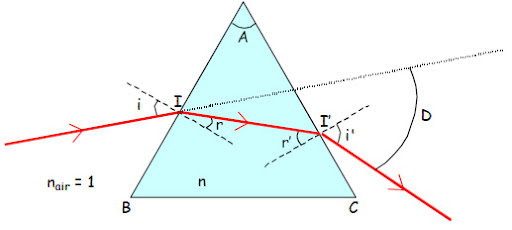
Cette figure apporte peu d'information et laisse supposer que le rayon réfracté à l'intérieur du prisme est perpendiculaire à la face d'entrée, ce qui a priori est faux. Je te fournis un schéma plus général. A toi d'adapter les notations à celles de ton problème.Avec les notations de la figure : pour i1=45°, tu peux calculer l'angle de réfraction (r ou r1). Il existe ensuite une relation simple entre l'angle au sommet, r et r'. Connaissant l'expression de r', tu peux en déduire une condition sur l'indice n pour qu'il y ait réfraction limite en I'. C'est ainsi que j'interprète ton énoncé car il n'est pas correctement posé : pour l'angle i=45° une réflexion totale sur la seconde face conduit à une inégalité vérifiée par n, pas à une valeur précise de n...