Inscription / Connexion Nouveau Sujet
Incertitude
Bonjour,
Je chercher à calculer des incertitudes, cependant j'ai un peu oublié, ces 2 méthodes sont-elles correctes ?
J'ai aussi entendu dire que l'incertitude d'une somme est la somme des incertitudes. Donc au lieu de la deuxième technique je peux calculer l'incertitude de ab/c avec la première technique et sommait l'incertitude de d ? Et pour les "..." je ne savais pas par quoi compléter
Merci d'avance
malou edit > **pour info ![]() **sujet verrouillé en maths, cela se traitera ici**
**sujet verrouillé en maths, cela se traitera ici**
Les deux méthodes conduisent au même résultat. Disons que la première est plus adaptée au calcul de l'incertitude absolue et que la seconde est plus adaptée au calcul de l'incertitude relative.
D'accord merci
Comme l'addition me pose probleme pour calculer avec les ln, est ce que je peux l'ignorer en faisant les calculs et à la fin rajouter ◇(d)/|d| ?
Les raisonnements sur les incertitudes ont évolués depuis quelques dizaines d'année. La méthode actuellement la plus utilisée actuellement conduits aux résultats suivants :
Pour l'incertitude absolue :
Pour l'incertitude relative :
On remplace les sommes par la racine carrée de la somme des carrés...
Comme l'addition me pose probleme pour calculer avec les ln, est ce que je peux l'ignorer en faisant les calculs et à la fin rajouter ◇(d)/|d| ?
Faire un calcul complet avec les différentielles est indispensables quand la même grandeur apparaît à la fois au numérateur et au dénominateur. Un exemple que tu peux essayer de traiter si tu as un peu de temps :
où a et b sont deux mesures indépendantes. La méthode de la différentiation logarithmique est la plus rapide pour obtenir l'incertitude relative sur f.
J'ai fait ça, je ne suis pas trop sûr pour la différentielle de ln(a+b), je dérive par rapport à a en laissant b constant puis multiplie par la différentielle de a et puis je bloque a et je dérive par rapport à b et je multiplie par db ?
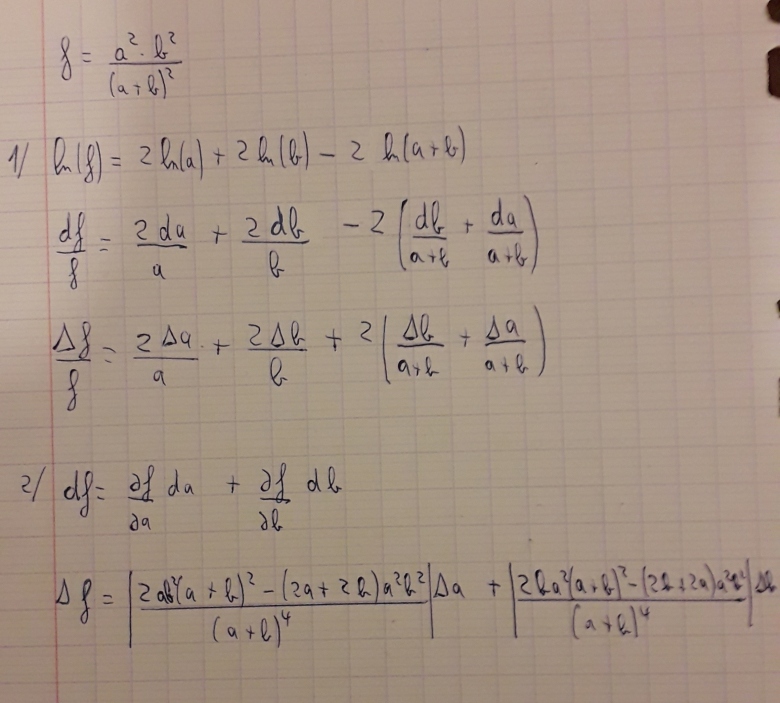
Attention au piège due à la présence de a et de b à la fois au numérateur et au dénominateur. Il faut simplifier la différentielle en regroupant les termes dépendants de da et les termes dépendants de db. Ce n'est qu'ensuite que l'on passe à l'incertitude relative.
La méthode est bonne. Fait comme le conseille ton professeur mais on obtient un résultat plus réaliste en remplaçant la somme par la racine carrée de la somme des carrés des deux incertitudes comme expliqué dans mon premier message.



