Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Impédance d'entrée d'un circuit

Posté par
Jean469 25-06-16 à 14:45

Bonsoir,
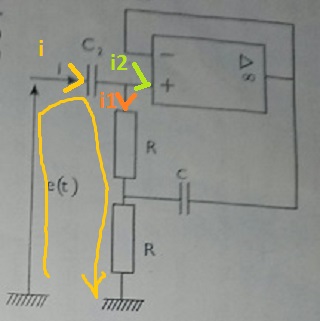
J'essaie de déterminer l'impédance d'entrée de ce circuit ci-dessous,en utilisant la loi des maille et des noeuds(c'est pas gagné) seulement,(Millman ferai l'affaire mais je ne maitrise pas assez bien).

Toutefois voici ce que j'ai pu dire:
La LDN donne: I=I1+I2 o I2=i+=i-=0,donc I=I1.

Et la LDM donne Ur1=Uc et e(t)=Uc2+Ur1+Ur2.

En 2) On demande la fréquence de résonance et le facteur de qualité Q.
Mais toute aide serai déjà bienvenue pour le 1).

Impédance d\'entrée d\'un circuit

Posté par
vanoisere : Impédance d'entrée d'un circuit 25-06-16 à 15:32

Bonjour
As-tu pris en compte le fait que le potentiel de la borne de droite de C est Vs=V- = V+ ???

Posté par
J-Pre : Impédance d'entrée d'un circuit 25-06-16 à 15:46

1)

L'ampli travaille dans sa zone linéaire et donc V- = V+ = Vs

i = jwC2.(e - Vs)
i2 = 0 (si ampli parfait)
i1 = (Vs-V1)/R
v1 = R.i4
i3 = jwC.(v1-Vs)
i = i1 + i2
i1 = i3 + i4

i = jwC2.(e - Vs)
i = (Vs-V1)/R
v1 = R.i4
i3 = jwC.(v1-Vs)
i = i3 + i4

Eliminer V1:
i = jwC2.(e - Vs)
i = (Vs-R.i4)/R = Vs/R - i4
i3 = jwC.(R.i4-Vs)
i = i3 + i4

Eliminer i3 et i4

i = jwC2.(e - Vs)
i = jwC.(R.(i - Vs/R)-Vs) + i - Vs/R

i = jwC2.(e - Vs)
0 = jwC.(R.i - 2.Vs) - Vs/R

i = jwC2.(e - Vs)
jwC.R.i = 2jwCVs + Vs/R

Eliminer i :
jwC.R . jwC2.(e - Vs) = 2jwCVs + Vs/R

j²w²C.C2.R.e = j²w²C.C².R.Vs  + 2jwCVs + Vs/R

Vs = j²w²C.C2.R.e/(j²w²C.C2.R + 2jwC + 1/R)

Vs = -w²C.C2.R.e/(1/R - w²C.C2.R + 2jwC)

i = jwC2.(e - vs)

i = jwC2.(e + w²C.C2.R.e/(1/R - w²C.C2.R + 2jwC))

i = e.jwC2.(1 + w²C.C2.R/(1/R - w²C.C2.R + 2jwC))

Zi = e/i

Zi = [1 + w²C.C2.R/(1/R - w²C.C2.R + 2jwC)]/(jwC2)

Zi = [1/R - w²C.C2.R + 2jwC + w²C.C2.R]/[(1/R - w²C.C2.R + 2jwC).(jwC2)]

Zi = [1/R + 2jwC]/[(1/R - w²C.C2.R + 2jwC).(jwC2)]

Brut de fonderie, sans aucune vérification ... et donc fautes de calcul incluses.



Impédance d\'entrée d\'un circuit

Posté par
vanoisere : Impédance d'entrée d'un circuit 25-06-16 à 17:04

Théorème de Millman appliqué au noeud commun aux deux résistances et à C :

V_{N}=\frac{\frac{V_{E+}}{R}+jC\omega V_{E+}}{\frac{2}{R}+jC\omega}=V_{E+}\cdot\frac{1+jRC\omega}{2+jRC\omega}
Loi d'Ohm appliquée à la résistance ” du haut ” :

i=\frac{V_{E+}-V_{N}}{R}=\frac{V_{E+}}{R}\left(1-\frac{1+jRC\omega}{2+jRC\omega}\right)=\frac{V_{E+}}{R}\cdot\frac{1}{2+jRC\omega}
Impédance de C2 :

i=jC_{2}\omega\left(e-V_{E+}\right)=jC_{2}\omega\cdot e-jC_{2}\omega\cdot R\cdot i\left(2+jRC\omega\right)
En regroupant les termes dépendant de i, on obtient l'impédance d'entrée :

Z_{e}=\frac{e}{i}=\frac{1+jRC_{2}\omega\left(2+jRC\omega\right)}{jC_{2}\omega}=2R+j\left(R^{2}C\omega-\frac{1}{C_{2}\omega}\right)

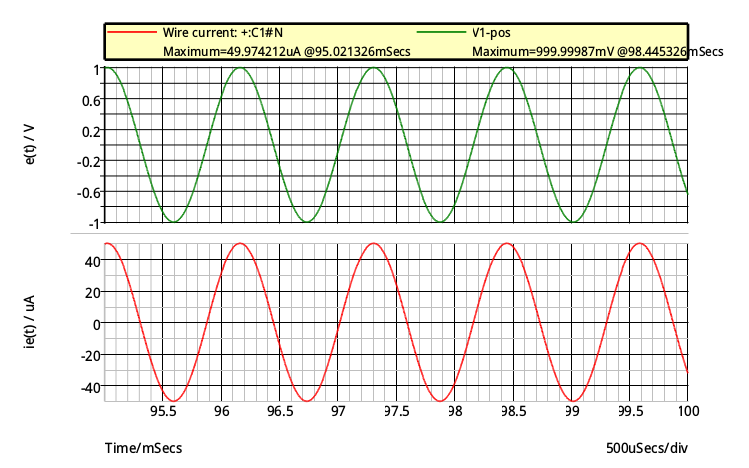
Comme le suggère la suite de l'énoncé, il existe une fréquence pour laquelle le module de l'impédance d'entrée présente un minimum. Cette fréquence particulière vérifie : R\sqrt{CC_{2}}\cdot2\pi\cdot f=1. L'impédance est alors réelle et égale à 2R, tension d'entrée et intensité d'entrée sont alors en phase. Pour illustrer cela, voici une simulation avec R = 10k ; C= 10nF ; C2=33nF. Pour f = 876Hz, on obtient bien i(t) et e(t) en phase . Pour une amplitude de la tension d'entrée de 1V, on obtient une amplitude de l'intensité de 50µA ; le rapport vaut bien 2R...

Impédance d\'entrée d\'un circuit

Posté par
vanoisere : Impédance d'entrée d'un circuit 26-06-16 à 07:38

Complément à mon message précédent : si le théorème de Millman te fait peur, tu peux appliquer la loi des nœuds au point N mais à condition de remplacer aussitôt les intensités par leurs expressions en fonction des potentiels et des impédances. Sinon tu introduis un certains nombre d'inconnues dans tes équations que tu risques d'avoir le plus grand mal à éliminer ensuite. Nous avons déjà eu ce genre de discussion me semble-t-il...
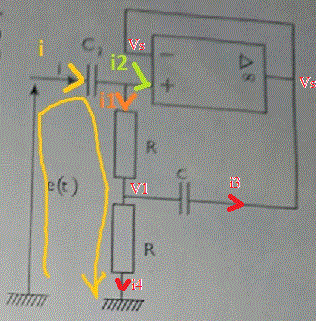
J'utilise les orientations des courants du schéma posté par JP le   25-06-16 à 15:46 mais je continue d'appeler N le nœud commun aux deux résistances et à C : VN = V1. J'utilise le fait que VS=VE+ :

i_{1}=i_{3}+i_{4}

\frac{V_{E+}-V_{N}}{R}=jC\omega\left(V_{N}-V_{S}\right)+\frac{V_{N}}{R}
Avec : V_{S}=V_{E+}, on obtient :

V_{N}\left(\frac{2}{R}+jC\omega\right)=V_{E+}\left(\frac{1}{R}+jC\omega\right)
Soit après multiplication de tous les termes par R :

V_{N}=V_{E+}\cdot\frac{1+jRC\omega}{2+jRC\omega}
On retrouve le théorème de Millman ; la suite est celle de mon message précédent.
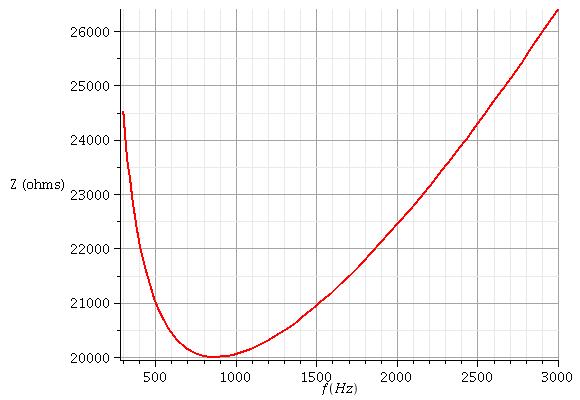
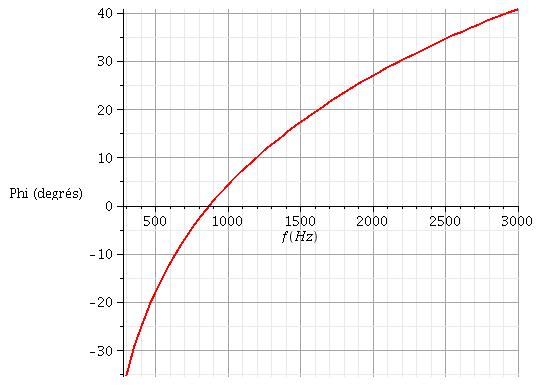
Voici la représentation graphique des variations en fonction de la fréquence du module Z et de l'argument phi de l'impédance d'entrée complexe pour les valeurs des composants déjà indiquées. Les courbes théoriques et les courbes simulées coïncident parfaitement tant que la fréquence reste suffisamment faible pour que l'ampli. op. fonctionne de façon quasi parfaite. On retrouve bien le cas particulier déjà évoqué pour f = 876Hz : Z=2R ; phi=0°.

Impédance d\'entrée d\'un circuit

Impédance d\'entrée d\'un circuit

Posté par
Jean469re : Impédance d'entrée d'un circuit 26-06-16 à 19:25

vanoise @ 25-06-2016 à 17:04

R\sqrt{CC_{2}}\cdot2\pi\cdot f=1.

Merci beaucoup pour ton aide,en gros pour le 2) j'en déduit que la fréquence de résonance c'est  f=\frac{1}{R\sqrt{CC_{2}}}.
Je n'ai plus qu'a trouvé le facteur de qualité Q alors!

Posté par
Jean469re : Impédance d'entrée d'un circuit 26-06-16 à 19:30

vanoise @ 26-06-2016 à 07:38

ensuite. Nous avons déjà eu ce genre de discussion me semble-t-il...

Ok merci,mais oui nous avons  déjà parler de ça , je ferai plus d'effort pour bien assimiler tout cela,ça doit être évident pour toi,mais ça l'est pas toujours pour moi.

Posté par
Jean469re : Impédance d'entrée d'un circuit 26-06-16 à 19:33

J-P @ 25-06-2016 à 15:46

1)L'ampli travaille dans sa zone linéaire et donc V- = V+ = Vs

Merci pour ton aide JP,content de te revoir sur le forum.

Posté par
vanoisere : Impédance d'entrée d'un circuit 26-06-16 à 22:11

Citation :
j'en déduit que la fréquence de résonance c'est  f=\frac{1}{R\sqrt{CC_{2}}}.

Attention à ne pas confondre fréquence et pulsation...
Citation :
Je n'ai plus qu'a trouvé le facteur de qualité Q alors!

N'ayant pas l'énoncé complet, il m'est difficile d'être précis... Pour un circuit résonant RLC  série en régime sinusoïdal établi  sous tension e(t) sinusoïdale, il est d'usage d'écrire l'expression du complexe associé à l'intensité instantanée i(t) sous la forme :

\boxed{\underline{i}=\frac{\underline{e}}{\underline{Z_{RLC}}}=\frac{\frac{\underline{e}}{R}}{1+jQ\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}=\frac{\frac{\underline{e}}{R}}{1+jQ\left(\frac{f}{f_{0}}-\frac{f_{0}}{f}\right)}}
Par analogie, il est possible ici de poser :

\boxed{\underline{i}=\frac{\underline{e}}{\underline{Z}}=\frac{\underline{e}}{2R+j\left(R^{2}C\omega-\frac{1}{C_{2}\omega}\right)}\frac{\frac{\underline{e}}{2R}}{1+j\left(\frac{RC\omega}{2}-\frac{1}{2RC_{2}\omega}\right)}=\frac{\frac{\underline{e}}{2R}}{1+jQ\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}=\frac{\frac{\underline{e}}{2R}}{1+jQ\left(\frac{f}{f_{0}}-\frac{f_{0}}{f}\right)}}
Nécessité cette fois de diviser tous les termes par 2R pour faire apparaître un "1" au dénominateur... Les valeurs de 0 et de f0 ont déjà été déterminées. Reste à déterminer Q en procédant pas identification...

Posté par
vanoisere : Impédance d'entrée d'un circuit 26-06-16 à 23:19

Manque un signe "égal" dans la dernière formule écrite à 22h11 :

\\ \\ \boxed{\underline{i}=\frac{\underline{e}}{\underline{Z}}=\frac{\underline{e}}{2R+j\left(R^{2}C\omega-\frac{1}{C_{2}\omega}\right)}=\frac{\frac{\underline{e}}{2R}}{1+j\left(\frac{RC\omega}{2}-\frac{1}{2RC_{2}\omega}\right)}=\frac{\frac{\underline{e}}{2R}}{1+jQ\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}=\frac{\frac{\underline{e}}{2R}}{1+jQ\left(\frac{f}{f_{0}}-\frac{f_{0}}{f}\right)}}

Posté par
J-Pre : Impédance d'entrée d'un circuit 27-06-16 à 13:06

Je recommence mes calculs avec un poil plus d'attention.

i = jwC2.(e - Vs)
i = (Vs-V1)/R
v1 = R.i4
i3 = jwC.(v1-Vs)
i = i3 + i4

On élimine V1 et i4 et on arrive à :
i = jwC2.(e-Vs)
i3 = -jwRC.i
2i = i3 + Vs/R

On élimine i3 :
i = jwC2.(e-Vs)
2i = -jwRCi + Vs/R

2.jwC2.(e-Vs) = -jwRC(jwC2.(e-Vs)) + Vs/R
...

Vs/e = [(2+jwRC).jwRC2]/(1-w²R²CC2 + 2jwRC2)

Avec i = (e-Vs).jwC2 -->

i = lwC2.e - jwC2.e.[(2+jwRC).jwRC2]/(1-w²R²CC2 + 2jwRC2)
Développer et simplifier -->
i = e.jwC2/(1-w²R²CC2 + 2jwRC2)

Ze = e/i = (1-w²R²CC2 + 2jwRC2)/(jwC2)

Posté par
Jean469re : Impédance d'entrée d'un circuit 27-06-16 à 17:31

vanoisevanoisevanoisevanoise

vanoise @ 26-06-2016 à 22:11

Citation :
j'en déduit que la fréquence de résonance c'est  f=\frac{1}{R\sqrt{CC_{2}}}.

Attention à ne pas confondre fréquence et pulsation...

Désolé j'ai oublié le 2pi sous la racine!
Euh le schéma 2 et l'exo complet c'est :

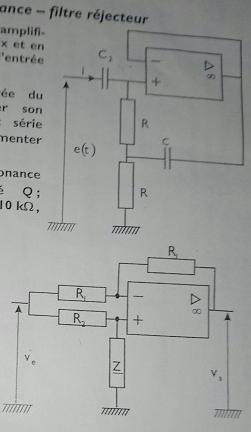
Impédance d\'entrée d\'un circuit

***Image recadrée***

Posté par
vanoisere : Impédance d'entrée d'un circuit 27-06-16 à 20:43

Bonjour
J'avais donc bien  "deviné" qu'il fallait faire une analogie avec  un circuit RLC série.. J'espère que tu as été capable tout seul de déterminer la valeur de Q. Avec les valeurs fournies des capacités de condensateurs, on obtient une valeur de Q très élevée caractéristique d'une résonance très aiguë...
Avec l'aide déjà apportée, j'espère que tu vas être capable seul de trouver la valeur de T. Puisque a priori, l'ampli op fonctionne en régime linéaire, la méthode est simple :
1° exprimer la tension VE- par le théorème de Millman ou la loi des noeuds comme je te l'ai expliqué ;
2° exprimer la tension VE+ : la méthode la plus simple consiste à considérer que l'ensemble {R2 , Z} se comporte en diviseur de tension : sinon : méthode précédente ;
3° écrire VE+=VE- et le tour est joué ! Bon courage !

Posté par
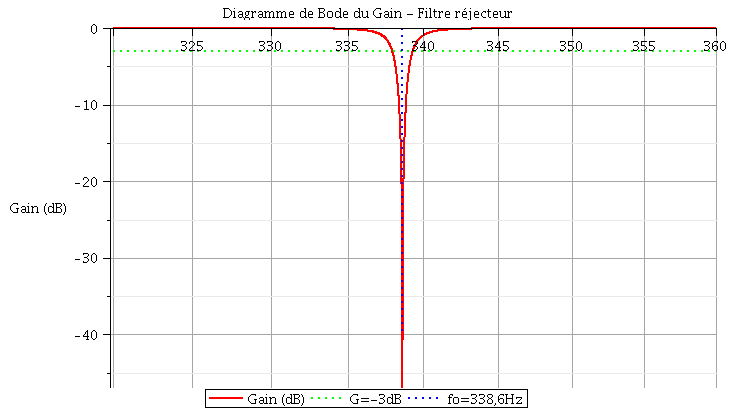
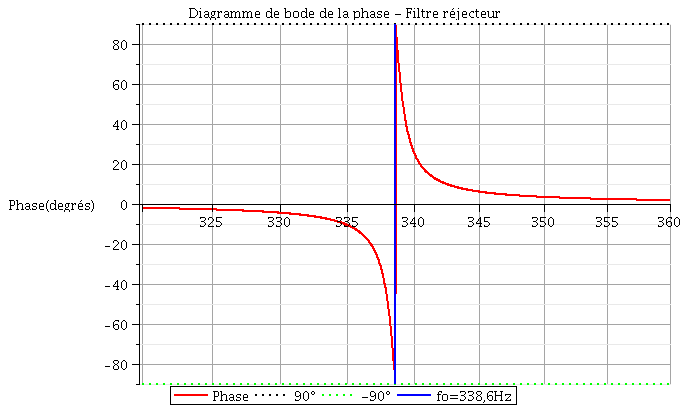
vanoisere : Impédance d'entrée d'un circuit 27-06-16 à 23:54

Voici les diagrammes de Bode qui pourront sans doute t'aider à la question 4 (même si celui de la phase ne semble pas demandé)...
A toi de retrouver tout cela par toi-même !

Impédance d\'entrée d\'un circuit

Impédance d\'entrée d\'un circuit

Posté par
J-Pre : Impédance d'entrée d'un circuit 28-06-16 à 13:04

Ze = e/i = (1-w²R²CC2 + 2jwRC2)/(jwC2)


(R'L'C' série) : R' + jwL' + 1/(jwC') = (jwR'C' - w²L'C' + 1)/(jwC') = (1 - w²L'C' + jwR'C')/(jwC')

On a donc :

C' = C2
L'C' = R²CC2
R'C' = 2RC2

C' = C2 (= 47 pF)
L' = R².C (= 4700 H)
R' = 2R (= 20 kohms)
------

3)

V+ = Ve . Z/(R2+Z)
V- = Ve + (1/2) * (Vs - Ve)

Ve . Z/(R2+Z) = Ve + (1/2) * (Vs - Ve)
Ve . Z/(R2+Z) = (1/2).Ve + Vs/2

Ve.[Z/(R2+Z) - 1/2] = Vs/2
Ve.[2Z/(R2+Z) - 1] = Vs
Ve.(Z-R2)/(R2+Z) = Vs
Vs/Ve = (Z-R2)/(R2+Z)

Vs/Ve = [(1 - w²L'C' + jwR'C')/(jwC') - R2]/[R2 + (1 - w²L'C' + jwR'C')/(jwC')]
Vs/Ve = [(1 - w²L'C' + jwC'(R'-R2)]/[1 - w²L'C' + jwC'(R'+R2)]

4)

A la résonnance, on a : Vs/Ve = [jwC'(R'-R2)]/[jwC'(R'+R2)] = (R'-R2)/(R'+R2)
|T| = 0 à la résonnance si R2 = R'

Avec R2=R' : Vs/Ve = (1 - w²L'C')/(1 - w²L'C' + 2j.wC'R')

Vs/Ve = (1 + 2,21.10^-7.(jw)²)/(1 + 1,88.10^-6.jw + 2,21.10^-7.(jw)²)

G = 20.log|1 - 2,21.10^-7.w²| - 20.log(V((1 - 2,21.10^-7.w²)² + (1,88.10^-6 . w)^2))

... qui donne ceci :

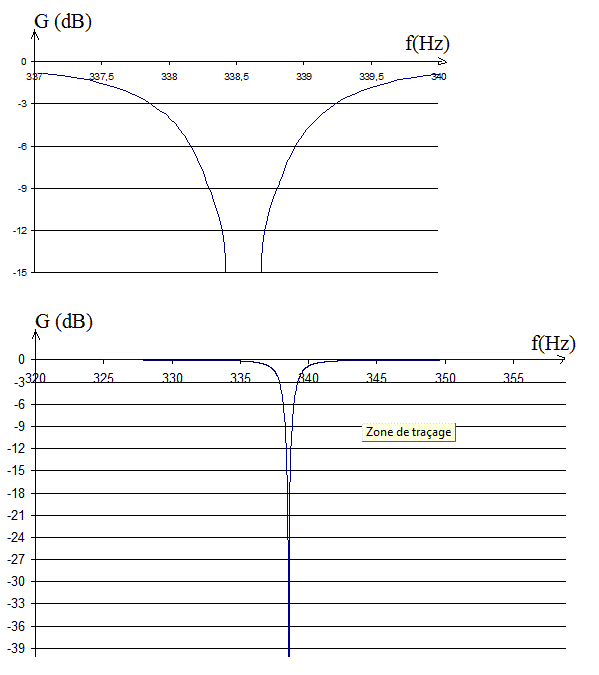
Impédance d\'entrée d\'un circuit

... toujours sans vérifications.

Posté par
vanoisere : Impédance d'entrée d'un circuit 28-06-16 à 14:18

Bonjour

Citation :
... toujours sans vérifications.

Pas très sympa pour moi cette remarque : le diagramme de Bode posté par JP est la copie conforme, me semble-t-il  , de celui que j'ai posté la veille....
Citation :
A toi de retrouver tout cela par toi-même !

C'est raté ! Mais enfin : jean469 est un étudiant sérieux !

Posté par
J-Pre : Impédance d'entrée d'un circuit 28-06-16 à 16:49

La plupart du temps, je ne vérifie pas mes réponses et je termine donc mes messages par "Sauf distraction" ou par "Calculs non vérifiés" ou par "... toujours sans vérifications" ou ...
pour avertir le lecteur qu'il NE DOIT PAS se contenter de recopier mes réponses sans travailler, il doit les  comprendre et les corriger si besoin est.  

Cela ne concerne en rien les messages d'autres intervenants.

Certes dans ce cas, le diagramme de Bode que je trouve a un air de famille avec celui de vanoise.
Néanmoins, ils sont tellement "sharp" qu'il est difficile d'être sûr, juste par les dessins de voir s'ils sont identiques ou bien seulement proches.

Ma remarque n'a donc rien à voir avec le message de vanoise ...

Quant à ma manière de répondre, elle n'a pas changé depuis bien longtemps ... et ne changera pas.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !