Inscription / Connexion Nouveau Sujet
Grille de résistances
Bonjour à tous, sur cet exercice, il s'agit de trouver la résistance équivalente entre A et B. Je sais que la réponse est Req = 0.5R mais je ne comprends pas pourquoi ma méthode ne marche pas.
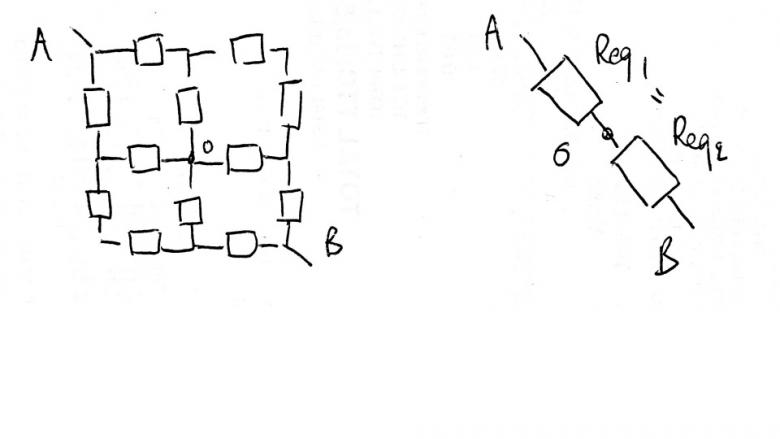
J'ai essayé de considérer un court circuit avec un point O, afin de trouver la résistance équivalente entre O et A, mais je n'ai pas le bon résultat...
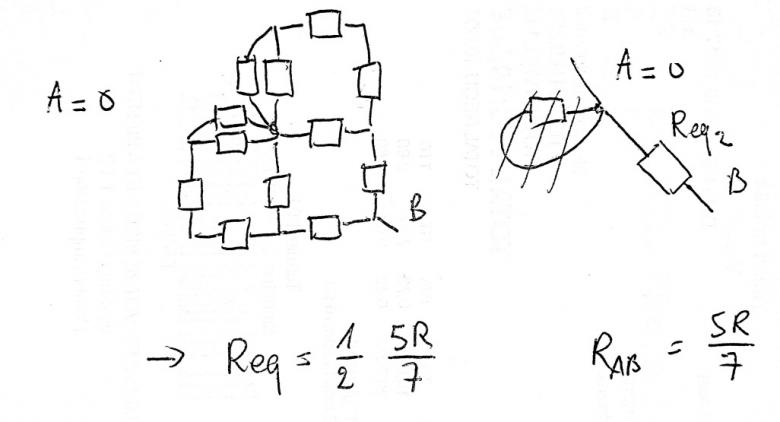
Je vous remercie d'avance pour votre aide.
PS : Je sais retrouver le résultat à l'aide de Kirschoff et par symétrie, inutile de m'en parler.
Bonsoir
L'axe AOB est axe de symétrie séparant le réseau en 2 moitiés . Deux noeuds symétriques par rapport à cet axe sont au même potentiel. Imagine que tu replies une moitié du réseau en le faisant tourner de 180° autour de l'axe de symétrie. Chaque noeud se retrouve ainsi au dessus d'un autre noeud au même potentiel. Tu peux alors imaginer de connecter deux à deux ces noeuds de même potentiel. La résistance du réseau n'est pas modifiée par cette opération car les fils de connection ne sont pas traversés par du courant.
Chaque résistance R se retrouve ainsi en parallèle avec une autre résistance R, l'ensemble des deux étant équivalente à R/2.
Bref: pour obtenir la résistance équivalente, tu peux supprimer une des deux moitiés du réseau à condition de remplacer dans la moitié restante R par R/2.
Cela donne :
Req= (R/2)+(R//R)+(R/2)=3R/2
Merci de votre réponse.
Donc si j'ai bien compris, dans ce cas ci, connecter les "points symétriques" est possible car ne change pas le potentiel (par égalité). Dans ce que j'ai fait ça ne marche pas parce que ça modifie le circuit. Pourtant, j'avais l'impression que c'était ce qui était utilisé pour démontrer Kenelly...
Je crois que tu as compris !
Pour le théorème de Kennely, une démonstration possible consiste à écrire que la résistance équivalente, vue de deux quelconques des trois bornes, la troisième borne étant déconnectée, est identique pour l'étoile et le triangle. Cela donne trois équations pour trois inconnues.


