Inscription / Connexion Nouveau Sujet
glissade circulaire
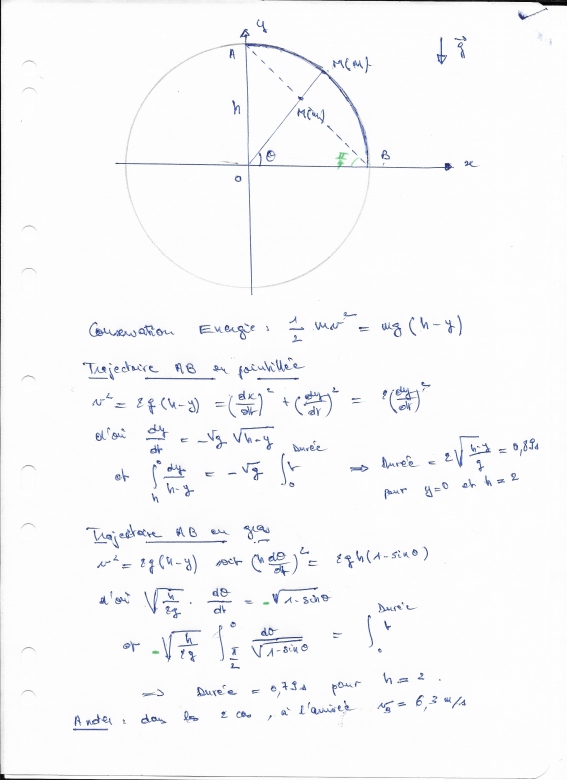
Bonjour, une masse m glisse sans frottement à l'intérieur d'un tuyau circulaire sur un quart de cercle de rayon 2 mètres ( donc dénivellé de 2 mètres avec une vitesse initiale nulle).J'ai calculé la durée de la descente et je trouve 0,79 s. Cela me parait faible, en effet : la durée d'une descente le long de la corde qui joint le quart de cercle dure quant à elle 0,89 s. La durée de la descente le long de l'arc de cercle ne devrait-elle pas être supérieure ? (intuitivement cela me parait évident mais je ne trouve pas d'erreur ou d'explication. Merci de votre réponse.
Bonjour
La trajectoire rectiligne n'est pas la trajectoire la plus rapide du point de vue du temps (la plus rapide est la cycloïde inversée : voir ici par exemple : 
)
Cela dit : peux-tu présenter rapidement ton calcul ? La situation est moins simple qu'il n'y parait.
Pour la trajectoire rectiligne, on obtient un peu plus rapidement le résultat en remarquant que le mouvement rectiligne est uniformément accéléré d'accélération g.sin(
/4=(g.
2)/2. On obtient ainsi très simplement une durée du trajet AB égal à :
Pour la trajectoire circulaire, les remarques de mon premier message supposaient un arc de cercle situé en dessous de la droite AB. Cela revient alors à trouver le quart de la période d'un pendule simple de longueur l=R avec une amplitude des oscillations égale à /2.
Avec ta trajectoire au-dessus de la droite AB, j'obtiens la même intégrale que toi, même si il est possible de l'obtenir un peu plus rapidement en utilisant les coordonnées polaires. Cependant un problème se pose : la position initiale est une position d'équilibre. Il s'agit d'un équilibre instable certes mais, sur le plan théorique, supposer la vitesse nulle en A conduit à l'absence de mouvement. D'ailleurs l'intégrale que tu as posée conduit logiquement à une durée infinie : le mobile n'arrive jamais en B ! Je serais curieux de savoir comment tu as obtenu ta valeur numérique.
Bonsoir à vous deux,
@pepeben : conformément au règlement, tu dois recopier tes pistes de réflexion (à l'exception du schéma, cela va de soi).
Tu as tous les utilitaires pour cela :
extrait de 
la FAQ du forum :Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
extrait de la FAQ du forum :Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
guide latex
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le 
mode d'emploi du forum
Bonjour,
Excusez-moi de ne avoir répondu hier mais j'avais d'autres affaires à traiter. Merci pour votre éclairage : effectivement la masse m placée sur le sommet du cercle subit une force résultante nulle et donc, soumise à aucune accélération, reste immobile. Mon erreur était de penser que l'intégrale put converger et m'a amené à un calcul trop approximatif des développements limités.
j'ai donc procédé à un nouveau calcul et j'arrive bien à une durée infinie si la borne inférieure est égale à pie/2. Ci-joint les principales étapes du calcul.
** image supprimée => dernier avertissement ... **
Calcul de
Je pose I =
remplacer
Je pose J =
remplacer
calculer I+J
calculer I-J
d'où I =1/2(I+J+I-J)
poser
= + infini
pour = 0,1 rd , on trouve une durée de glissade de 1,38 s
pour = 0,01 rd , on trouve une durée de glissade de 2,41 s
Ok. Très astucieuse ta méthode !
Comme déjà suggéré,tu peux étudier le cas où l'arc de cercle est en dessous de AB ( symétrique par rapport à AB de l'arc que tu viens d'étudier). Tu va pouvoir démontrer que la trajectoire rectiligne n'est pas nécessairement la plus rapide.
pour résoudre le cas du quart de cercle inférieur ne faut-il pas savoir calculer
? cette intégrale est-elle calculable ?
Le problème est analogue à l'étude d'un pendule de grande amplitude(/2). L'équation différentielle vérifiée par l'angle polaire n'admet pas de solution explicite et l'intégrale à calculer, qui fait effectivement intervenir l'inverse de , n'admet pas de solution exacte. Il faut se contenter d'une solution numérique approchée. J'ai eu l'occasion de développer cela à propos du pendule. Il suffit ici de choisir une amplitude de
/2. Voir à partir de la page 10 ; le reste est hors sujet.
Vu - je ne connaissais pas cette formule de BORDA.
appliqué à mon cas (h=2m; g=9,81)cela me donne une durée de descente de 0,82s par défaut si j'ai bien suivi votre démonstration.
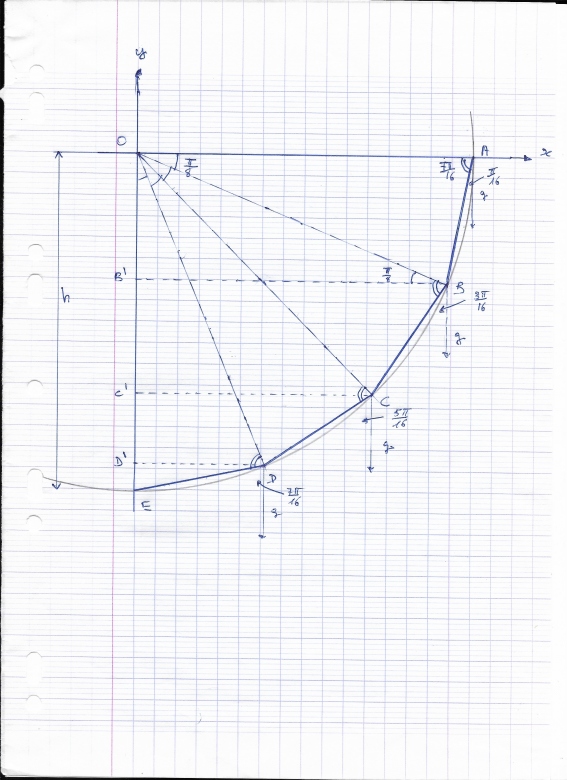
J'ai pour ma part fait l'approximation graphique suivante:
Je divise le quart de cercle inférieur en 4 angles égaux et je fais glisser la masse le long des cordes AB,BC,CD,DE en supposant une continuité des vitesses aux points B,C,D.
La longueur totale des cordes = 0,781x4 = 3,124m pour une longueur de l'arc AE de pi = 3,141m ( les longueurs sont très proches)
Je calcule la durée de glissade le long de chaque corde et je trouve une durée totale de 0,40 + 0,17 + 0,14 + 0,13 = 0,84s par excès.
La vérité doit se trouver entre les deux résultats. Bien entendu mon approximation ne peut se faire que pour un cas particulier et la vôtre a vocation à une application générale.
En tous cas j'ai les réponses aux questions posées pour ce qui concerne ces figures de glissade et je vous remercie pour votre aide.
Annuler
connectez vous