Inscription / Connexion Nouveau Sujet
gain et phase
SALUT
SVP est ce que vous pouvez m'aimer à calculer le gain et la phase de ce schéma sachant que OTA il e comporte comme un amplificateur opérationnel
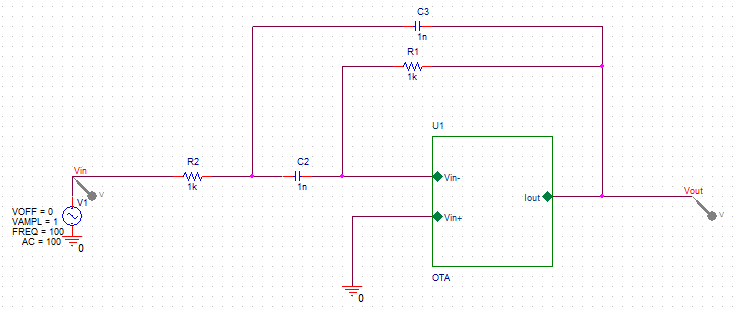
je l'ai appliqué deja mais ca e donne pas la bonne reponse, probablement que j'ai tort dans une phase de calcul
Ou bien raisonner en courant.
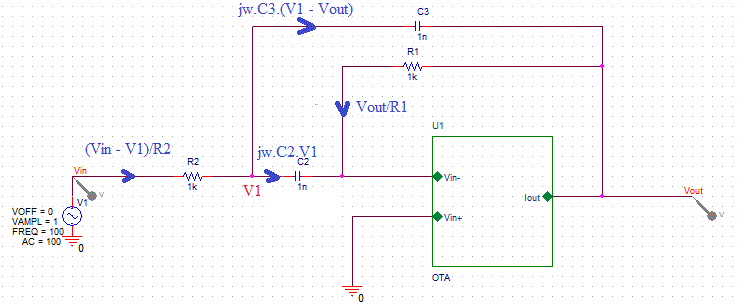
Equations des 2 noeuds :
(Vin - V1)/R2 = jwC2.V1 + jwC3.(V1 - Vout)
jwC2.V1 = - Vout/R1
Vin/R2 - V1/R2 = jwC2.V1 + jwC3.V1 - jwC3.Vout
V1 = - Vout/(jwR1C2)
Vin/R2 + jwC3.Vout = V1(1/R2 + jwC2 + jwC3)
Vin/R2 + jwC3.Vout = - Vout/(jwR1C2) * (1/R2 + jwC2 + jwC3)
Vin/R2 = -Vout * (jwC3 + (1/R2 + jwC2 + jwC3)/(jwR1C2))
Vin/R2 = -Vout * (j²w²R1C2C3 + 1/R2 + jwC2 + jwC3)/(jwR1C2)
Vout/Vin = -jwR1C2/[R2.(j²w²R1C2C3 + 1/R2 + jwC2 + jwC3)]
Vout/Vin = -jwR1C2/(1 + jwR2(C2+C3) + j²w²R1R2C2C3)
-----
Calculs non vérifiés.

mariemj connais le théorème de Millmann qui conduit au résultat en 3 lignes.
Ce genre t'intervention...
Garde tes remarques stupides pour toi.
Mon calcul est archi détaillé (même si pas vérifié) et peut tout aussi bien être fait en 3 lignes avec un rien d'habitude.
Ce n'est pas parce que les profs n'enseignent qu'une seule méthode qu'il n'en existe pas d'autres tout aussi bonnes et performantes.
Le déclin est bien marqué ... certains profs n'y sont malheureusement pas pour rien.

Merci eidos : enfin un peu d'humour et de bonne humeur.
Pour terminer la réponse à ce problème : que mariemj utilise la méthode préconisée par son professeur. Dans tous les cas, on obtient la fonction de transfert suivante :
S'il s'agit seulement de faire l'application numérique pour une fréquence de 100Hz soit une pulsation de 628rad/s, on peut faire les constatations suivantes :
On remarque :
On en déduit l'expression approchée de la fonction de transfert :
Ce sont sensiblement les valeurs que j'obtiens à l'aide d'un logiciel de simulation. Pour une amplitude en entrée de 1V, j'obtiens en sortie une amplitude de 628µV et la tension de sortie est en quadrature de phase retard sur la tension d'entrée : à un extremum d'une tension, correspond une valeur nulle de l'autre tension.
La solution de vanoise est fausse.
Il suffit de prendre un cas particulier évident pour le montrer, soit par exemple le cas avec C3 = 0 (donc condensateur C3 non présent)
On a alors directement H = -R1/(R2 + 1/(jwC2))
H = -jwR1C2/(1 + jwR2C2)
La solution du message du 11-10-15 à 18h19 dans laquelle on ferait C3 = 0, donnerait H = -jwR1C2 ... ce qui n'est pas correct.
La solution du message 10-10-15 à 20:02 dans laquelle on ferait C3 = 0, donnerait H = -jwR1C2/(1 + jwR2C2).
Cela ne prouve pas que ma solution est correcte, mais montre en tous cas que celle de vanoise est fausse.
Le " Dans tous les cas, on obtient la fonction de transfert suivante : ... " me semble alors bien hasardeux.

J.P. a raison : son argument sur le cas particulier C3 = 0 est imparable. Ma phrase : "Dans tous les cas, on obtient la fonction de transfert suivante : " a été écrite parce que justement les deux méthodes conduisent au même résultat. En revanche, j'ai commis une étourderie en recopiant la formule de la fonction de transfert sous Latex : j'ai effectivement oublié un terme en C2. Je présente mes excuses pour cette étourderie. On obtient donc dans tous les cas :
La suite reste valable.
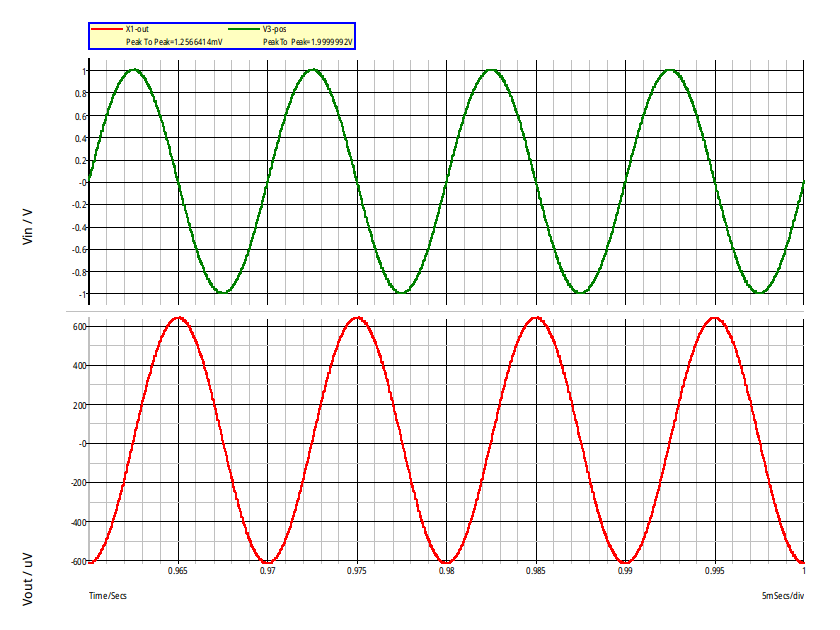
Voici ce que donne la simulation :
Ce genre t'intervention...
Garde tes remarques stupides pour toi.
 :?
:? On se détend, une nouvelle semaine commence
On se détend, une nouvelle semaine commence 
Certains (surtout dans les profs) sont donneurs de leçons, très souvent mal placées.
Ils ne supportent pas qu'on sortent des sentiers battus et veulent se cantonner dans les oeillères de l'enseignement actuel ... dont on voit les résultats dans la médiocrité croissante.
On applique des "formules" toutes faites en supprimant tout raisonnement.
J'essaie donc, quand je le peux, de donner des alternatives à la courte vue de l'enseignement actuel en appliquant des voies de résolutions différentes.
Alors, quand certains critiquent cette manière d'ouverture d'esprit que je tente de donner, cela me hérisse.
Que chacun réponde comme il l'entend sans critiquer stupidement les réponses des autres et tout sera pour le mieux.
Cela ne veut pas dire qu'il ne faut pas corriger les erreurs manifestes faites dans d'autres réponses, cela n'a rien à voir avec les critiques stériles sur les méthodes utilisées par d'autres utilisant des voies différentes à celles étriquées enseignées.

Biensur, le but d'un forum est d'être un lieu d'échange, et dans un échange, il y a souvent des opinions divergentes, c'est d'ailleurs tout l'intérêt, mais seulement on peut ne pas etre d'accord sans dire que l'autre personne est stupide, ou pire, je lis parfois des jugements encore plus durs sur des réponses, entre membres du sites qui interviennent souvent, et parfois même cela débouche sur des désinscriptions, et je déplore qu'on puisse en arriver là quand on intervient sur un forum pour discuter avec des gens qui ont les mêmes centres d'intérêts...
Bref, l'idée ici n'est pas de jeter de l'huile sur le feu, mais bien l'inverse, alors je retourne m'occuper de mes oignons, il y a de belles annonces à venir prochainement concernant les sites, mais avant celà, il faut que je bosse !! 

Merci pour tte les reponses
ca ma vraiment bcp servis,
mais cette fois si on considere que Iout=gm(V+-V-)??
tant que gm c'est la transconductance de l'ampli?
Bonsoir,
J'imagine que la sortie de ton montage est reliée à un dipôle récepteur ou aux bornes d'entrées d'un quadripôle : Que peut-on dire de l'impédance de ce dipôle ou de l'impédance d'entrée de ce quadripôle ?
Je voulais juste savoir si le montage se "prolonge" vers la droite afin de quantifier un éventuel courant de sortie par la borne Vout. Peut-être peut-on considérer ce courant d'intensité nulle ou au moins d'intensité négligeable devant l'intensité du courant sortant de OTA ???
Je suis revenu à ta première phrase du premier message :
sachant que OTA il e comporte comme un amplificateur opérationnel
Tous les calculs ont été menés en tenant compte de cette hypothèse, en particulier du fait que Vin+=Vin-. Cela n'est pas le cas avec un amplificateur à transductance. Il faut reprendre tous les calculs...
Je trouvais étonnant aussi qu'un montage tout de même assez complexe se réduise au final, compte tenu des valeurs numériques, à un simple dérivateur inverseur...
oui au debu c'etai le cas qu'il se comporte comme un amplificateur ideal tel que V+=V-
mais les résultats theoriques ne correspond pas au résultats pratique
donc il faut maintenant introduire la transconductance gm
et en meme temps je cherche comment en peux calculer gm d'un mirroir de courrent Wilsom simple et cascode et je trouve aucune relation!!!!
Bonsoir,
mais cette fois si on considere que Iout=gm(V+-V-)??
tant que gm c'est la transconductance de l'ampli?
Là, le calcul est beaucoup plus compliqué car on ne peut plus poser Vin-=0 !
Méthode possible (je ne suis pas du tout certain que ce soit la meilleure car je la trouve tout de même bien longue) :
Je fais l'hypothèse qu'aucun courant ne sort par Vout et que le courant d'entrée dans l'ampli en Vin- est d'intensité nulle. Je note i1 et i3 les intensités traversant les branches R1 et C3 toutes deux orientées de la droite vers la gauche. Je ne mets pas les barres sous les complexes pour alléger l'écriture.
Vues des bornes IN et OUT le circuit est équivalent à R2 en série avec la mise en parallèle de C3 avec (R1 série C2), l'ensemble étant parcourue par (i1+i3). On peut calculer l'impédance équivalente Ze de cette association.
Vout-Vin=Ze.(i1+i3)=-Ze.gm.Vin-
Cela nous donne une première expression de Vin- en fonction de Vout, Vin et les caractéristiques du circuit.
Etape suivante : par l'application du théorème de Millman ou par toute autre méthode, on peut obtenir une autre expression de Vin- en fonction de Vout, Vin, des R des C et de w.
En identifiant les deux expressions de Vin- on obtient la fonction de transfert recherché.
Remarque : le cas de l'ampli op idéal correspond à Vin-=0 avec i2+i3
 0. la fonction de transfert obtenue précédemment doit donc être la limite du résultat actuel lorsque gm tend vers l'infini.
0. la fonction de transfert obtenue précédemment doit donc être la limite du résultat actuel lorsque gm tend vers l'infini.
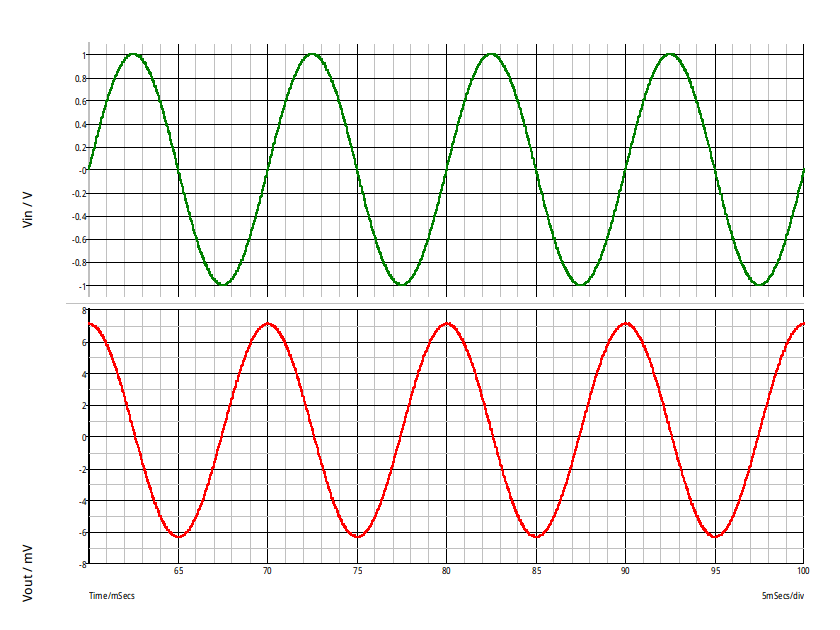
J'ai tenté une simulation : elle ne correspond pas nécessairement à ce que tu as obtenu en TP car je n'ai aucune indication sur l'intensité du courant de commande de l'amplificateur à transductance. J'ai trouvé comme précédemment deux tensions en quadrature de phase mais un gain nettement plus important.
merci pour votre réponse, moi je travaille dans le domaine fréquentielle
je trace DB(Vout/Vin) en frequence
Bonsoir,
moi je travaille dans le domaine fréquentielle
je trace DB(Vout/Vin) en frequence
Je t'ai fourni l'exemple d'un signal d'entrée sinusoïdal parce que c'est l'indication fournie pour Vin sur ton premier schéma.
Mais les indications de mon dernier post te permettent d'obtenir la fonction de transfert, donc de tracer le diagramme de Bode si nécessaire. Cependant, pour un tracé précis, il faudrait plus de renseignements sur gm
j'ai u des dificulté en calculant la fonction de transfert on introduisant gm?
est ce que c'est possible de me donner plus d'indication sur comment je vais la calculer
Voici quelques éléments de calculs. Les explications correspondantes sont fournies dans mon message posté le 21-10-15 à 23:41.
En éliminant V1 entre les deux dernières équations, tu obtiens une seconde expression de Vin- en fonction de Vin, Vout ,w , C3, C2, R1, R2.
En écrivant l'égalité des deux expressions de Vin- , tu obtiens la fonction de transfert. Le calcul littéral est long et fastidieux. Il se simplifie grandement si on suppose, comformément au schéma que tu as fourni : R1 = R2 et C2 = C3.
Tu obtiens a priori un filtre passe-bande mais sans information complémentaire sur gm et la façon dont l'amplificateur à transductance est alimenté en courant, je ne peux rien dire de certain.


