Inscription / Connexion Nouveau Sujet
Freinage par induction
Bonsoir,
Je rencontre un problème sur un exercice traitant du freinage par induction.
Je dois étudier le mouvement d'une spire MNPQ de longueur b et largeur a en translation selon l'axe (Ox), de masse m, résistance R et inductance négligeable.
Celle-ci va entrer dans une zone d’abscisse comprise entre 0 et d (d > b) soumise à un champ B = B.ez
L’abscisse de l'avant de la spire en repéré par X(t). On note v sa vitesse.
un schéma ici: 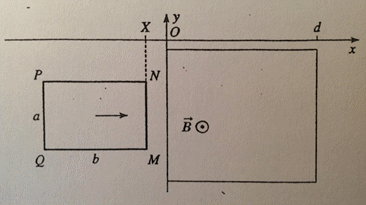
J'ai du décomposer le mouvement selon 5 phases (avant et après la zone, pendant l'entrée et la sortie, et dans la zone), et établir dans chacun des cas s'il y avait ou non induction, la fem, l'intensité induite et les résultantes de laplace qui en découlait le cas échéant.
Je dois ensuite exprimer les équations différentielles vérifiées par v(t) et v(X).
Je trouve donc qu'il n'y a induction que pendant l'entrée et la sortie.
Celles-ci sont caractérisées par une résultante de la Laplace de type "F = -k.v" et il y a bien freinage.
Je n'ai pas de problème particulier pour l'équation différentielle vérifiée par v(t), j'applique le PFD et je trouve:
(*)
Le problème survient pour trouver l'équation différentielle vérifiée par v(X).
J'ai trouvé un semblant de méthode: écrire que:
puis vient:
Alors là je ne comprends pas du tout la dernière étape.
D'où vient le résultat ?
Je suppose que ce serait en disant que vérifie la première équation différentielle (*) puis en simplifiant par v(t), mais je ne vois pas du tout pourquoi
vérifierait (*).
Donc si quelqu'un a une idée 
Merci.
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
bonsoir,
dv/dt = dv/dX . dX/dt
et
dv/dt = -k/m v (je te fais confiance 
donc dv/dX = -k/m v/v = -k/m
sauf erreur
Ce que je ne comprends pas c'est que v est une fonction de deux variables différentes (X et t) selon les cas, donc en quoi avons nous le droit d'écrire "dv/dt = -k/m v" où pour que la troisième égalité soit vraie, ce serait un v(X) ?
Merci en tout cas de prendre du temps.
Ce que je ne comprends pas c'est que v est une fonction de deux variables différentes (X et t) selon les cas
oui, le physicien cherche non seulement la fonction mais aussi la variable la plus adéquate pour décrire les phénomènes
et la notation différentielle lui permet de "changer de variable" sans trop de soucis
en écrivant par ex.
dv/dt = dv/dX . dX/dt
à gauche v=v(t)
à droite v=v(X), choix plus judicieux (pour ce problème particulier) car dv/dX = -k/m = cst
je te conseille d'aller faire un tour ici:
l'auteur explique cet aspect de la notion de différentielle beaucoup mieux que je ne pourrais le faire


